Automatic calculation of myocardial perfusion reserve using deep learning with uncertainty quantification

Introduction

Magnetic resonance (MR) perfusion imaging is non-invasive without ionizing radiation and is reported to show non-inferior performance in the prediction of major cardiac events, when compared with the invasive fractional flow measurement (1). Quantitative analysis of myocardial perfusion with MR imaging (MRI) helps evaluate diffuse microvascular dysfunction, and it requires many steps to arrive at perfusion quantification (2,3). Automatic analysis of myocardial perfusion with artificial intelligence has been demonstrated in the literature, showing the potential to improve efficiency in cardiac MRI exams (4-7). The myocardial perfusion reserve index (MPRI) based on myocardial upslope estimation is used as a means to assess perfusion reserve (8). Myocardial perfusion imaging under stress and rest conditions is necessary for the estimation of the MPRI. Stress perfusion is indispensable for the visual identification of ischemic and salvageable tissue. Rest perfusion has its value in quantitative studies, although it alone does not provide sufficient diagnostic accuracy for ischemia detection from visual analysis (9). For instance, MR images are prone to signal intensity variation across the myocardium due to the sensitivity of the surface coil array, but the normalization of the regional upslope by rest perfusion can reduce the effect of intensity variation and thus improve the accuracy of quantitative perfusion measurement.

MPRI measurements have been used to evaluate perfusion abnormalities due to coronary microvascular dysfunction in patients with severe aortic stenosis (AS) (10) and hypertrophic cardiomyopathy (HCM) (11), and in women with symptoms of ischemia and no obstructive coronary artery disease (CAD) (12). They have also been used to standardize acquisition protocols for an alternative stress agent such as regadenoson (13). However, one primary drawback in the context of analysis technology is that the MPRI quantification process typically involves laborious and time-consuming procedures, including manual tracings of the epicardial and endocardial borders in dynamic contrast-enhanced (DCE) images (14).

Fully automatic MPRI estimation would be desirable, since it does not require the annotator’s effort and time for tracing the myocardial contours and annotating landmarks of the left ventricle (LV) center point and anterior right ventricle (RV) insertion point. Recent studies investigated the feasibility of automatic analysis of MPRIs based on myocardial blood flow (MBF) (5,15), but to our knowledge there has been lack of studies in automatic estimation of MPRI based on the myocardial upslope estimates. Our work aimed to develop a new automatic algorithm for MPRI estimation and evaluate its performance against a semi-automatic reference method, which involves manual adjustments of the myocardial segmentation results and frame ranges of the LV and myocardial upslopes.

Methods

Data acquisition

Cardiac MRI scans were performed on a 1.5 T scanner (Siemens Avanto, Erlangen, Germany). The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). The study was approved by the institutional ethics board of the Samsung Medical Center, and individual consent for this retrospective analysis was waived. An electrocardiogram (ECG) gated gradient echo sequence was employed to obtain DCE images during first pass of extracellular contrast agent. Imaging parameters were the following: flip angle =15°, slice thickness =8 mm, field-of-view (FOV) =400×315 mm², image matrix =320×252, pixel spacing =1.25×1.25 mm², and number of image frames =80. As the acquisition took longer than a minute, the subject resumed breathing after a 15–20 s of breath-hold. Frame-by-frame motion compensation was performed using a non-rigid registration algorithm (16). We used motion-compensated perfusion Digital Imaging and Communications in Medicine (DICOM) data for this study.

Image processing overview

A flowchart of the proposed method is illustrated in Figure 1. It describes a fully automatic process of measuring the upslope value from stress perfusion data. The automatic process involves the automatic detection of an RV enhanced frame using k-means clustering (17), Monte-Carlo dropout U-Net for myocardial segmentation (18), landmark localization using machine learning (19), and finally, segmental calculation of myocardial upslope values. The final MPRI value is calculated as a ratio of the upslope value from stress perfusion to the upslope value from rest perfusion in each myocardial segment.

Figure 1 A flowchart of the proposed method. The flowchart shows an automatic estimation of myocardial upslope for stress perfusion, with a series of k-means clustering, Monte-Carlo dropout U-Net, and machine learning landmark detection. This process is repeated for rest perfusion. The final MPRI value for a given myocardial segment is calculated as a ratio of Upslope_stress to Upslope_rest. DCE, dynamic contrast-enhanced; RV, right ventricle; LV, left ventricle; MR, magnetic resonance; MPRI, myocardial perfusion reserve index; a.u., arbitrary unit.

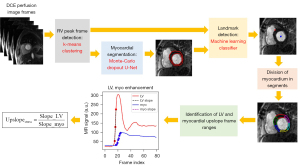
Detection of peak RV enhancement frame

The detection of an RV enhanced frame can lead to the detection of subsequent LV and myocardial enhanced frames, and it was performed using the k-means clustering algorithm available on scikit-learn library (20). Each data sample consisted of an 80×1 vector of a time series signal from a voxel. The number of clusters was empirically set to 4 for the identification of the RV region of interest (ROI). A cluster corresponding to the RV ROI was obtained by finding a cluster c_min that is the smallest in the calculation of the cost function F(c) shown in Eq. [1].

F(c)=1T∑t=1Tt⋅fc(t)+α⋅argmaxt(fc(t))+β⋅1max(fc(t))−min(fc(t))[1]

cmin=argmincF(c)[2]

f_c(t) is the normalized time intensity curve (TIC) averaged from the pixels that belong to a cluster c. The first term is the first moment of f_c(t), which is a metric suitable to the detection of the arterial input function (AIF) in cerebral perfusion (21). The second term is a time index of the maximum f_c(t), weighted by α. It is used to penalize the late enhanced TIC, which is contributed by a cluster consisting of parts from the LV cavity. The third term is used to avoid the selection of a cluster resulting from the bright signal (e.g., subcutaneous fat). We tested two different sets of choice (α, β) = (0, 80) and (20, 80) to observe the effect of the second term on accuracy of peak RV frame detection. As shown in Figure 2, the peak RV enhancement frame t_RV was obtained by finding the time index of the peak signal enhancement from the cluster c_min in Eq. [2]. The peak RV frame detection step is used to develop a landmark detection model for localizing the anterior RV insertion point (see “Landmark localization” section) and to find an LV enhanced frame and a frame range for the LV upslope calculation (see “MPRI calculation” section).

Figure 2 Detection of an RV enhanced frame using k-means clustering. (A) Mean cluster signals after k-means clustering. The red line is a time intensity curve of a cluster corresponding to the RV cavity, and it results in the minimum cost value according to Eqs. [1] and [2]. The blue line, green line and black line represent time intensity curves of the other three clusters, and they result in higher cost values than the red line. (B) Detection of the maximum frame index (black dot) from the ‘RV’ time intensity curve. (C) The RV enhancement frame image from the detected frame in (B). Detected RV enhanced frames are used to train a machine learning model for localizing the anterior RV insertion point or to predict the anterior RV insertion point using the model on a test image. MR, magnetic resonance; a.u., arbitrary unit; RV, right ventricle.

Myocardial segmentation

We used the U-Net architecture (22) with dropout (23), which was trained on the cardiac cine MRI data (18,24). The segmentation model was trained on 13,535 short-axis slice cine images from 88 subjects and validated on 4,148 short-axis slice cine images from 22 subjects as described in (18). Hence, a total of 110 subjects were used for the myocardial segmentation model development (Table 1). The dropout ratio ranged from 0.1 to 0.3, following the implementation of the concrete dropout (25). We used a Monte Carlo dropout (26,27) for uncertainty estimation with 50 repetitions, where the output of the U-Net model was obtained with dropout (i.e., random selections of the units in each layer) for each repetition. From the results of the Monte Carlo dropout, we obtained average and standard deviation (SD) maps, denoted by AVG_MC (x, y) and SD_MC (x, y), respectively. For each time frame of interest, the pixel-wise summation of the SD map was calculated as a metric of uncertainty, denoted by relative sum of standard deviation (rSSD).

rSSD=∑x=1M∑y=1NSDMC(x,y)∑x=1M∑y=1NAVGMC(x,y)[3]

where N and M are the numbers of image rows and columns, respectively. The denominator of Eq. [3] penalizes the case where the contrast enhancement is minimal. We computed the rSSD metric for each time frame within the frame range of [t_RV+ 4, t_RV + 24]. Selection of a frame for an endocardial (or epicardial) boundary segmentation was made based on a frame that resulted in the smallest rSSD in the frames of interest. The stress and rest perfusion data of 60 subjects were used to evaluate the segmentation accuracy in terms of Dice similarity coefficient (28).

Landmark localization

We considered machine learning for automatic landmark localization (29). The LV center point was detected by calculating the center of gravity of the endocardial mask estimated using the deep learning segmentation described in the previous section. The RV insertion point was detected using random forest classifiers on the RV enhancement frame. The details of the landmark localization method followed the procedures described in (19). The main idea was to find candidate voxels that are likely to be the RV insertion point using a random forest classifier and calculate the center of gravity within the candidate voxels. In this work, we separately trained random forest classifier models for stress and rest perfusion data (Table 1). The stress perfusion data from 72 subjects were used to train a model, and the rest perfusion data from 63 subjects were used to train a model. The remaining 60 subjects’ data were used to test the two models on stress and rest perfusion data, respectively.

MPRI calculation

Based on the locations of the LV center point and RV insertion point, the myocardium was divided into six uniform segments (Figure 3). For each of the six myocardial segments, a mean time-intensity curve of the myocardial segment (TIC_{myo, k}) was obtained after averaging all the voxels within the k^th segment. Similarly, a mean time-intensity curve of the LV blood pool was obtained after averaging all the voxels within the LV blood pool. The frame ranges of the LV upslope and myocardial upslope were set to [t_RV− 3, t_LV + 3] and [t_LV− 3, t_LV + 10], respectively. The first derivative of the TIC was calculated. If the difference signal was less than 30% of the maximum difference value, it was not considered for the calculation of the upslope. A linear regression was performed on the upslope samples to estimate the slope and intercept. This process was performed on both stress and rest perfusion data, and the final MPRI value for the k^th myocardial segment was calculated as follows:

MPRIk=Upslopestress,kUpsloperest,k=Slopestress,kSlopestress,LVSloperest,kSloperest,LV[4]

Figure 3 Sample results of the presented automatic method from a patient for (A) stress and (B) rest perfusion data. The left column shows endocardial (red) and epicardial (green) contours as well as LV center point (red) and RV insertion point (green). The middle column shows automatic division of the myocardium into the six regions. The right column shows automatic selection of the upslope range in time as well as automatic estimation of the slopes for the time intensity curves of the LV blood pool (red) and a myocardial section (blue). LV, left ventricle; RV, right ventricle; MR, magnetic resonance; a.u., arbitrary unit.

Evaluation

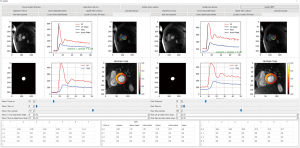
We developed a tool that involves the user’s epi/endocardial segmentation and landmark annotation for MPRI calculation. The tool is based on a Python custom user interface that allows for the semi-automatic assessment of MPRI (Figure 4). In the user interface, the user selects an image frame that shows adequate contrast between the myocardium and blood, clicks the button for the U-Net segmentation, and performs manual corrections of the myocardial contours if necessary. Next, the user annotates the two landmarks of an LV center point and an anterior RV insertion point. The user adjusts the frame ranges corresponding to the LV and myocardial upslopes. The above procedures are performed for stress and rest perfusion data. Finally, clicking the ‘Update MPRI’ button enables MPRI values of the six segments to be displayed in the panel. The MPRI estimates obtained by manual procedures served as a reference.

Figure 4 The custom user-interactive graphical user interface. This was used to calculate the MPRI values and served as the manual reference method. The layout shows both stress and rest perfusion analysis procedures in a window panel, which facilitates the direct comparison of the images and intermediate results between stress and rest perfusion. LV, left ventricle; MPRI, myocardial perfusion reserve index.

Landmark localization accuracy was evaluated by the Euclidean distance from the manually annotated location to the machine learning predicted location. The distance errors were calculated for the LV center point and the anterior RV insertion point, for both the stress and rest perfusion data.

MPRI calculations were performed on the 60 test subjects who underwent both stress and rest perfusion scans. Among the 60 test subjects, there were 34 patients with CAD, 19 patients with HCM, 3 patients with AS, 3 patients with cardiac amyloidosis (AMYL), and 1 healthy volunteer (VOL). Computation time of the proposed method was measured on a Microsoft Windows 10 operating system with an eight-core AMD Ryzen 7 1800X CPU @ 3.60 GHz, 16 GB RAM, and NVIDIA GeForce GTX 1080 GPU (8 GB memory size). Mean MPRI values were calculated from all segments in each patient. The test subjects were divided into three groups: (I) diffuse ischemic pattern group; (II) focal ischemic pattern group; and (III) “other” group. The diffuse ischemic pattern group included HCM, AS, AMYL, and 2- or 3-vessel disease CAD patients. The focal ischemic pattern group included CAD patients with 1-vessel disease. The “other” group included patients suspected of CAD and the healthy VOL.

Statistical analysis

Statistical analysis was performed using the R software (R Foundation for Statistical Computing, Vienna, Austria). The intraclass correlation coefficient (ICC) and its 95% confidence interval (CI) were computed between two methods in terms of MPRIs. The mean and SD values were calculated for MPRIs. A two-sample unpaired Student’s t-test was performed to determine if MRPI values between two groups were significantly different. A P value <0.05 was considered to indicate a statistically significant correlation, given the null hypothesis of no relationship between the two measurements.

Results

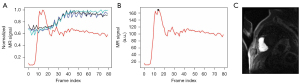
For the peak RV enhanced frame detection, the choice (α, β) = (0, 80) in Eq. [1] resulted in an accuracy of 101/120=84.2%, and the choice (α, β) = (20, 80) resulted in an accuracy of 120/120=100%. Figure 5 illustrates examples of correct and incorrect RV enhanced frame detection results. Figure 5A shows the same successful detection results for both (α, β) = (0, 80) and (20, 80). Figure 5B shows a correct detection of the peak RV enhanced frame with the choice (α, β) = (20, 80). Figure 5C shows an incorrect detection of the peak RV enhanced frame, where the LV ROI was detected after k-means clustering. The inclusion of the second term in Eq. [1] helped to robustly find the peak RV enhanced frame.

Figure 5 Impact of the choice of (α, β) in Eq. [1] on peak RV enhanced frame detection. (A) Successful detection for both (α, β) = (0, 80) and (20, 80) in Test 19 subject. (B) Successful detection for (α, β) = (20, 80) in Test 23 subject. (C) Unsuccessful detection for (α, β) = (0, 80) in Test 23 subject. The results of (B) and (C) were obtained from the same subject. The failed detection in (C) originates from the wrong selection of a minimum cluster index, implying the importance of the second term in Eq. [1]. RV, right ventricle.

For the landmark localization task with the 60 test subjects, the median (interquartile range) values of distance errors were 2.3 mm (1.5–3.7 mm) for the RV insertion point and 2.2 mm (1.5–3.0 mm) for the LV center point, for the stress perfusion data. For the rest perfusion data, the median (interquartile range) values of distance errors were 5.3 mm (3.9–7.3 mm) for the RV insertion point and 2.7 mm (1.8–3.5 mm) for the LV center point.

When compared with manual segmentation of the 60 test subjects, the deep learning-based automatic segmentation of the myocardium using Monte-Carlo dropout resulted in median (interquartile range) Dice similarity scores of 0.80 (0.77–0.84) for stress perfusion and 0.81 (0.77–0.84) for rest perfusion. The results were similar to those of our previous work where Dice similarity scores had a mean ± SD value of 0.806±0.096 (18).

MPRI measurements using the proposed technique correlated with manual reference in segmental assessment (ICC =0.75, 95% CI: 0.70–0.79, P<0.001). Figure 6A shows a scatter plot of correlation between automatic and reference MPRI measurements. In the Bland-Altman analysis, the automatic and reference MPRI values were in agreement in per-segment [MPRI: mean difference =−0.02, 95% limits of agreement = (−0.86, 0.82)] (see Figure 6B). More specifically, Table 2 shows segment-wise evaluations of the MPRIs. The anterior segment showed the lowest ICC of 0.63, while the infero-lateral segment showed the highest ICC of 0.82. The antero-septal segment showed the largest mean difference, while the infero-lateral segment showed zero mean difference. The diffuse group’s mean MPRI was smaller than the focal group’s mean MPRI (mean ± SD, 1.37±0.47 vs. 1.71±0.56, P=0.032). The “other” group’s MPRIs were not statistically different from the diffuse (P=0.933) or the focal ischemic groups (P=0.060). The “other” group’s mean MPRI was comparable to the diffuse group’s mean MPRI (mean ± SD, 1.38±0.32 vs. 1.37±0.47, P=0.933). The automatic method took approximately 96 s to estimate an MPRI from stress and rest perfusion data, and the Monte-Carlo U-Net segmentations in the stress and rest perfusion images took up 95% of the computational time.

Figure 6 Comparison of segmental MPRIs between the manual and automatic measurement methods. (A) Scatter plot of the MPRI measurements. (B) Bland-Altman plot of the MPRI measurements. The colors of the dots indicate the myocardial segments. MPRI, myocardial perfusion reserve index.

Figure 7 shows three representative examples of the MPRI measurements. The blue arrows indicate the splenic switch-off in stress perfusion and the splenic enhancement in rest perfusion, suggesting that the adenosine stress condition was well maintained during the stress perfusion scan (30). Figure 7A shows a healthy VOL case, where the MPRIs in all segments are higher than 1. Figure 7B shows a perfusion defect case in the left circumflex (LCx) artery territory, which appears dark in the lateral myocardial segment in stress perfusion image and appears normal in rest perfusion image. MPRI was the lowest with the value of 0.35. Figure 7C shows a three-vessel disease case, having distributed stress perfusion defects in the three main artery territories, and a normal appearance in the rest perfusion. The MPRI values of Figure 7B,7C are relatively lower in the entire myocardium than those of Figure 7A.

Figure 7 Sample cases. (A) A healthy volunteer case; (B) a case of perfusion defect (yellow arrow) in the LCx territory; (C) a case of perfusion defect (yellow arrow) in three vessel diseases. The blue arrows in (A) indicate the splenic switch-off in adenosine stress relative to the rest perfusion. The splenic switch-off in stress perfusion images implies the adequacy of adenosine stress. The MPRI color coded maps overlaid to the perfusion images show high values in (A) and relatively low values in (B,C). The antero-lateral region in (B) resulted in the lowest MPRI value of 0.35. MPRI, myocardial perfusion reserve index; LCx, left circumflex artery.

Discussion

In this study, we proposed a method that automatically calculates the MPRI using a series of processing pipelines, consisting of RV peak frame detection with k-means clustering, automatic myocardial segmentation with Monte-Carlo dropout U-Net, landmark localization with random forest classifiers, and frame range detection for the myocardial upslope estimation. A moderate correlation of MPRIs was observed between the proposed method and manual method. The proposed method demonstrated its feasibility to automate MPRI quantification. MPRI quantification would be tedious and time consuming if it involved manual segmentations of the myocardium, manual annotations of the landmark points, and manual adjustments of the upslope frame ranges in the contrast enhancement curves.

Similar to our study, recent studies have investigated the feasibility of automatic methods for the analysis of DCE perfusion MRI. Scannell et al. demonstrated the utility of deep learning-based methods for myocardial segmentation, landmark localization of the RV insertion point, and AIF estimation to automatically and accurately quantify MBF values averaged over each myocardial segment (4,7), but the estimation of MPRI based on myocardial upslope estimates was not demonstrated in their work. Xue et al. used deep learning for automatic myocardial segmentation and MBF estimation (31) as well as for automatic landmark localization (32). Jacobs et al. showed automatic myocardial segmentation in perfusion (33). Our study is different from the other methods because we used myocardial segmentation based on Monte-Carlo dropout U-Net and calculated myocardial upslopes for the MPRI estimation rather than MBFs.

We calculated the MPRI based on the ratio of stress perfusion upslope to rest perfusion upslope. Alternatively, one can consider measuring the MPRI based on the ratio of the stress perfusion MBF to the rest perfusion MBF. The main difference in the two MPRI calculations is whether to use the semiquantitative upslope or the quantitative MBF. It appears difficult to decide which one is more advantageous than the other, given the lack of standardization in cardiac MR perfusion image acquisition and analysis protocol. Hsu et al. compared MPRI values between two MPRI calculation methods using a dual bolus approach and concluded that the upslope-based MPRI method significantly underestimated MPRIs compared to the MBF-based MPRI method (34). However, Larghat et al. compared reproducibility between the two MPRI calculation methods and concluded that the semiquantitative analysis based on normalized upslope was more reproducible than quantitative method based on absolute MBF using Fermi-constrained deconvolution (35). Brown et al. compared reproducibility between stress (or rest) MBF and MPRI derived from stress and rest MBF ratios and concluded that both rest and stress MBF showed better repeatability than MPRI (36). Notably, recent review papers (6,37) indicate that semiquantitative analysis has limitations in nonlinearity between upslope and flow rates, and quantitative analysis requires dedicated acquisition protocols such as dual sequence (38) or contrast agent injection schemes such as dual bolus (34). Hence, dedicated perfusion acquisition and analysis methods would favor the quantitative MBF-based approach. The perfusion sequence protocol used in our study was based on neither dual sequence nor dual bolus, so we only considered the semiquantitative method to derive the MPRIs in this study.

Our study demonstrated the segmental analysis of MPRIs in the myocardium. The segmental analysis may average healthy myocardial voxels and ischemic myocardial voxels within a myocardial segment, hence leading to underestimation of myocardial ischemia in the presence of small ischemic lesions. Pixel-wise analysis (39) is an alternative method that overcomes the limitation of segmental analysis and has the potential to provide a focal ischemic lesion analysis automated with k-means clustering (40). Pixel-wise or subsegmental analysis enables the calculation of transmurality of ischemia and can improve diagnostic accuracy for the detection of obstructive CAD (41). A drawback of the pixel-wise perfusion quantification is its sensitivity to noise (42,43).

There are several factors that can contribute to the errors or uncertainties in MPRI estimates. First, the motion compensation from the scanner may not always remove 100% of inter-frame motion, and our method may be sensitive to any residual motion in the data. In our acquisition protocol, the acquisition took longer than a minute. The subject initially performed a breath-hold of 15–20 s in an initial stage of data acquisition, and then resumed free breathing until the end of the scan. Since the LV and myocardial enhancements during first pass typically occur during a subject’s breath-hold, the frame ranges corresponding to the LV and myocardial upslopes are not affected by breathing motion. Hence, we think that in general, upslope estimation is not highly likely to be affected by motion. Second, in some rare cases, the anatomical short-axis slices can be slightly different between stress and rest perfusion data. This may be due to the patient’s motion during a time interval between the stress and rest perfusion scan sessions. Errors in motion correction in either stress or rest perfusion data may contribute to the errors in the MPRI measurements (5). Third, a surface coil intensity correction was not used in this study. However, since the segmental MPRIs involve the division of stress upslopes by rest upslopes, coil sensitivity effect can be canceled out by the division. Fourth, the LV enhancement upslope reaches its peak within a very short duration. The temporal resolution of an R-R interval in the first pass perfusion may not be adequate for certain patients with low heart rates. Fifth, myocardial TICs may not show clear upslope patterns, especially in regions with low perfusion or ischemia. In this low perfusion case, it is often not straightforward to determine how to estimate the myocardial upslope.

The current study has limitations. First, a small number of subjects were employed, and the study was a single-center, single-vendor study. Second, deep learning segmentation models were trained on cardiac cine data, so it would improve segmentation accuracy if deep learning models were trained on cardiac perfusion data. Third, we considered the basal or mid slice level for the evaluation, not the apical slice level. Fourth, the MPRI manual calculations were performed by only one operator. The inter-operator agreement was not assessed in this study. Fifth, we considered motion-corrected perfusion image series data only. A recent study investigated the effectiveness of deep learning for motion correction in perfusion data (44). For the raw perfusion image series without inter-frame motion correction, it is worth investigating the effectiveness of motion correction algorithms (45) as a part of the processing workflow. Last but not least, we only compared the automatic MPRI calculation method with the reference MPRI calculation manually performed by an expert. We did not evaluate diagnostic accuracy by comparing it with the ground truth MPRI measurements using positron emission tomography or microspheres.

Conclusions

The proposed method automatically quantifies the MPRI measurements based on segmental upslopes obtained from stress and rest perfusion MRI data. The method utilizes a series of machine learning techniques consisting of k-means clustering for the RV peak frame detection, machine learning for the landmark localization, and Monte-Carlo dropout U-Net for the myocardial segmentation. The evaluation resulted in good correlation between the automatic method and the manual reference method. The method holds the potential to quantitatively assess myocardial ischemia without any user intervention, although it requires further investigation using multi-center, multi-vendor perfusion MRI data.

Acknowledgments

Funding: This research was supported by the “Regional Innovation Strategy (RIS)” through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (MOE) (No. 2022RIS-005).

Footnote

Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://qims.amegroups.com/article/view/10.21037/qims-23-840/coif). The authors have no conflicts of interest to declare.

Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). The study was approved by institutional ethics board of the Samsung Medical Center and individual consent for this retrospective analysis was waived.

Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.

References

1. Nagel E, Greenwood JP, McCann GP, Bettencourt N, Shah AM, Hussain ST, et al. Magnetic Resonance Perfusion or Fractional Flow Reserve in Coronary Disease. N Engl J Med 2019;380:2418-28. [Crossref] [PubMed]
2. Li XM, Jiang L, Min CY, Yan WF, Shen MT, Liu XJ, Guo YK, Yang ZG. Myocardial Perfusion Imaging by Cardiovascular Magnetic Resonance: Research Progress and Current Implementation. Curr Probl Cardiol 2023;48:101665. [Crossref] [PubMed]
3. Jerosch-Herold M, Seethamraju RT, Swingen CM, Wilke NM, Stillman AE. Analysis of myocardial perfusion MRI. J Magn Reson Imaging 2004;19:758-70. [Crossref] [PubMed]
4. Scannell CM, Veta M, Villa ADM, Sammut EC, Lee J, Breeuwer M, Chiribiri A. Deep-Learning-Based Preprocessing for Quantitative Myocardial Perfusion MRI. J Magn Reson Imaging 2020;51:1689-96. [Crossref] [PubMed]
5. Knott KD, Seraphim A, Augusto JB, Xue H, Chacko L, Aung N, Petersen SE, Cooper JA, Manisty C, Bhuva AN, Kotecha T, Bourantas CV, Davies RH, Brown LAE, Plein S, Fontana M, Kellman P, Moon JC. The Prognostic Significance of Quantitative Myocardial Perfusion: An Artificial Intelligence-Based Approach Using Perfusion Mapping. Circulation 2020;141:1282-91. [Crossref] [PubMed]
6. Seraphim A, Knott KD, Augusto J, Bhuva AN, Manisty C, Moon JC. Quantitative cardiac MRI. J Magn Reson Imaging 2020;51:693-711. [Crossref] [PubMed]
7. Scannell CM, Alskaf E, Sharrack N, Razavi R, Ourselin S, Young AA, Plein S, Chiribiri A AI-AIF. artificial intelligence-based arterial input function for quantitative stress perfusion cardiac magnetic resonance. Eur Heart J Digit Health 2023;4:12-21. [Crossref] [PubMed]
8. Narang A, Blair JE, Patel MB, Mor-Avi V, Fedson SE, Uriel N, Lang RM, Patel AR. Myocardial perfusion reserve and global longitudinal strain as potential markers of coronary allograft vasculopathy in late-stage orthotopic heart transplantation. Int J Cardiovasc Imaging 2018;34:1607-17. [Crossref] [PubMed]
9. Pons-Lladó G, Kellman P. State-of-the-Art of myocardial perfusion by CMR: A practical view. Reviews in Cardiovascular Medicine 2022;23:325.
10. Ahn JH, Kim SM, Park SJ, Jeong DS, Woo MA, Jung SH, Lee SC, Park SW, Choe YH, Park PW, Oh JK. Coronary Microvascular Dysfunction as a Mechanism of Angina in Severe AS: Prospective Adenosine-Stress CMR Study. J Am Coll Cardiol 2016;67:1412-22. [Crossref] [PubMed]
11. Kim EK, Lee SC, Chang SA, Jang SY, Kim SM, Park SJ, Choi JO, Park SW, Jeon ES, Choe YH. Prevalence and clinical significance of cardiovascular magnetic resonance adenosine stress-induced myocardial perfusion defect in hypertrophic cardiomyopathy. J Cardiovasc Magn Reson 2020;22:30. [Crossref] [PubMed]
12. Thomson LE, Wei J, Agarwal M, Haft-Baradaran A, Shufelt C, Mehta PK, Gill EB, Johnson BD, Kenkre T, Handberg EM, Li D, Sharif B, Berman DS, Petersen JW, Pepine CJ, Bairey Merz CN. Cardiac magnetic resonance myocardial perfusion reserve index is reduced in women with coronary microvascular dysfunction. A National Heart, Lung, and Blood Institute-sponsored study from the Women's Ischemia Syndrome Evaluation. Circ Cardiovasc Imaging 2015;8:e002481. [Crossref] [PubMed]
13. Bhave NM, Freed BH, Yodwut C, Kolanczyk D, Dill K, Lang RM, Mor-Avi V, Patel AR. Considerations when measuring myocardial perfusion reserve by cardiovascular magnetic resonance using regadenoson. J Cardiovasc Magn Reson 2012;14:89. [Crossref] [PubMed]
14. Agarwal M, Shufelt C, Mehta PK, Gill E, Berman DS, Li D, Sharif B, Li N, Bairey Merz CN, Thomson LE. Cardiac risk factors and myocardial perfusion reserve in women with microvascular coronary dysfunction. Cardiovasc Diagn Ther 2013;3:146-52. [Crossref] [PubMed]
15. Seraphim A, Dowsing B, Rathod KS, Shiwani H, Patel K, Knott KD, Zaman S, Johns I, Razvi Y, Patel R, Xue H, Jones DA, Fontana M, Cole G, Uppal R, Davies R, Moon JC, Kellman P, Manisty C. Quantitative Myocardial Perfusion Predicts Outcomes in Patients With Prior Surgical Revascularization. J Am Coll Cardiol 2022;79:1141-51. [Crossref] [PubMed]
16. Xue H, Zuehlsdorff S, Kellman P, Arai A, Nielles-Vallespin S, Chefdhotel C, Lorenz CH, Guehring J. Unsupervised inline analysis of cardiac perfusion MRI. Med Image Comput Comput Assist Interv 2009;12:741-9.
17. Xue H, Brown LAE, Nielles-Vallespin S, Plein S, Kellman P. Automatic in-line quantitative myocardial perfusion mapping: Processing algorithm and implementation. Magn Reson Med 2020;83:712-30. [Crossref] [PubMed]
18. Kim YC, Kim KR, Choe YH. Automatic myocardial segmentation in dynamic contrast enhanced perfusion MRI using Monte Carlo dropout in an encoder-decoder convolutional neural network. Comput Methods Programs Biomed 2020;185:105150. [Crossref] [PubMed]
19. Kim YC, Chung Y, Choe YH. Automatic localization of anatomical landmarks in cardiac MR perfusion using random forests. Biomedical Signal Processing and Control 2017;38:370-8.
20. Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, Blondel M, Prettenhofer P, Weiss R, Dubourg V. Scikit-learn: Machine learning in Python. Journal of Machine Learning Research 2011;12:2825-30.
21. Mouridsen K, Christensen S, Gyldensted L, Ostergaard L. Automatic selection of arterial input function using cluster analysis. Magn Reson Med 2006;55:524-31. [Crossref] [PubMed]
22. Ronneberger O, Fischer P, Brox T, editors. U-net: Convolutional networks for biomedical image segmentation. International Conference on Medical Image Computing and Computer-Assisted Intervention; 2015: Springer; 2015.
23. Srivastava N, Hinton G, Krizhevsky A, Sutskever I, Salakhutdinov R. Dropout: A simple way to prevent neural networks from overfitting. The Journal of Machine Learning Research 2014;15:1929-58.
24. Kim YC, Kim KR, Choi K, Kim M, Chung Y, Choe YH. EVCMR: A tool for the quantitative evaluation and visualization of cardiac MRI data. Comput Biol Med 2019;111:103334. [Crossref] [PubMed]
25. Gal Y, Hron J, Kendall A. editors. Concrete dropout. Advances in Neural Information Processing Systems; 2017.
26. Gal Y, Ghahramani Z. editors. Dropout as a bayesian approximation: Representing model uncertainty in deep learning. International Conference on Machine Learning; 2016.
27. Leibig C, Allken V, Ayhan MS, Berens P, Wahl S. Leveraging uncertainty information from deep neural networks for disease detection. Sci Rep 2017;7:17816. [Crossref] [PubMed]
28. Dice LR. Measures of the amount of ecologic association between species. Ecology 1945;26:297-302.
29. Stern O, Marée R, Aceto J, Jeanray N, Muller M, Wehenkel L, Geurts P. editors. Automatic localization of interest points in zebrafish images with tree-based methods. Pattern Recognition in Bioinformatics: 6th IAPR International Conference, PRIB 2011, Delft, The Netherlands, November 2-4, 2011. Delft: Springer; 2011.
30. Manisty C, Ripley DP, Herrey AS, Captur G, Wong TC, Petersen SE, Plein S, Peebles C, Schelbert EB, Greenwood JP, Moon JC. Splenic Switch-off: A Tool to Assess Stress Adequacy in Adenosine Perfusion Cardiac MR Imaging. Radiology 2015;276:732-40. [Crossref] [PubMed]
31. Xue H, Davies RH, Brown LAE, Knott KD, Kotecha T, Fontana M, Plein S, Moon JC, Kellman P. Automated Inline Analysis of Myocardial Perfusion MRI with Deep Learning. Radiol Artif Intell 2020;2:e200009. [Crossref] [PubMed]
32. Xue H, Artico J, Fontana M, Moon JC, Davies RH, Kellman P. Landmark Detection in Cardiac MRI by Using a Convolutional Neural Network. Radiol Artif Intell 2021;3:e200197. [Crossref] [PubMed]
33. Jacobs M, Benovoy M, Chang LC, Corcoran D, Berry C, Arai AE, Hsu LY. Automated Segmental Analysis of Fully Quantitative Myocardial Blood Flow Maps by First-Pass Perfusion Cardiovascular Magnetic Resonance. IEEE Access 2021;9:52796-811.
34. Hsu LY, Rhoads KL, Holly JE, Kellman P, Aletras AH, Arai AE. Quantitative myocardial perfusion analysis with a dual-bolus contrast-enhanced first-pass MRI technique in humans. J Magn Reson Imaging 2006;23:315-22. [Crossref] [PubMed]
35. Larghat AM, Maredia N, Biglands J, Greenwood JP, Ball SG, Jerosch-Herold M, Radjenovic A, Plein S. Reproducibility of first-pass cardiovascular magnetic resonance myocardial perfusion. J Magn Reson Imaging 2013;37:865-74. [Crossref] [PubMed]
36. Brown LAE, Onciul SC, Broadbent DA, Johnson K, Fent GJ, Foley JRJ, Garg P, Chew PG, Knott K, Dall'Armellina E, Swoboda PP, Xue H, Greenwood JP, Moon JC, Kellman P, Plein S. Fully automated, inline quantification of myocardial blood flow with cardiovascular magnetic resonance: repeatability of measurements in healthy subjects. J Cardiovasc Magn Reson 2018;20:48. [Crossref] [PubMed]
37. Dewey M, Siebes M, Kachelrieß M, Kofoed KF, Maurovich-Horvat P, Nikolaou K, et al. Clinical quantitative cardiac imaging for the assessment of myocardial ischaemia. Nat Rev Cardiol 2020;17:427-50. [Crossref] [PubMed]
38. Kellman P, Hansen MS, Nielles-Vallespin S, Nickander J, Themudo R, Ugander M, Xue H. Myocardial perfusion cardiovascular magnetic resonance: optimized dual sequence and reconstruction for quantification. J Cardiovasc Magn Reson 2017;19:43. [Crossref] [PubMed]
39. Hsu LY, Jacobs M, Benovoy M, Ta AD, Conn HM, Winkler S, Greve AM, Chen MY, Shanbhag SM, Bandettini WP, Arai AE. Diagnostic Performance of Fully Automated Pixel-Wise Quantitative Myocardial Perfusion Imaging by Cardiovascular Magnetic Resonance. JACC Cardiovasc Imaging 2018;11:697-707. [Crossref] [PubMed]
40. Daviller C, Grenier T, Ratiney H, Sdika M, Croisille P, Viallon M. Automatic myocardial ischemic lesion detection on magnetic resonance perfusion weighted imaging prior perfusion quantification: A pre-modeling strategy. Comput Biol Med 2019;110:108-119. Erratum in: Comput Biol Med 2019;114:103455. [Crossref] [PubMed]
41. Le MTP, Zarinabad N, D'Angelo T, Mia I, Heinke R, Vogl TJ, Zeiher A, Nagel E, Puntmann VO. Sub-segmental quantification of single (stress)-pass perfusion CMR improves the diagnostic accuracy for detection of obstructive coronary artery disease. J Cardiovasc Magn Reson 2020;22:14. [Crossref] [PubMed]
42. Zarinabad N, Chiribiri A, Hautvast GL, Ishida M, Schuster A, Cvetkovic Z, Batchelor PG, Nagel E. Voxel-wise quantification of myocardial perfusion by cardiac magnetic resonance. Feasibility and methods comparison. Magn Reson Med 2012;68:1994-2004. [Crossref] [PubMed]
43. Zarinabad N, Chiribiri A, Hautvast GL, Breeuwer M, Nagel E. Influence of spatial resolution on the accuracy of quantitative myocardial perfusion in first pass stress perfusion CMR. Magn Reson Med 2015;73:1623-31. [Crossref] [PubMed]
44. Sandfort V, Jacobs M, Arai AE, Hsu LY. Reliable segmentation of 2D cardiac magnetic resonance perfusion image sequences using time as the 3rd dimension. Eur Radiol 2021;31:3941-50. [Crossref] [PubMed]
45. Scannell CM, Villa ADM, Lee J, Breeuwer M, Chiribiri A. Robust Non-Rigid Motion Compensation of Free-Breathing Myocardial Perfusion MRI Data. IEEE Trans Med Imaging 2019;38:1812-20. [Crossref] [PubMed]