
Calibration phantom-based prediction of CT lung nodule volume measurement performance
Introduction
Obtaining accurate size and size change measurements of sub-centimeter lung nodules in low-dose computed tomography (CT) scans is essential for effective low dose CT lung cancer screening. Radiation dose delivered to patients must be minimized, typically following As Low As Reasonably Achievable (ALARA) guidelines (1), while maintaining high CT image quality to enable precise and accurate measurement of nodule volumes. Although currently available CT scanners provide tools for estimating radiation dose, there are no corresponding tools for estimating the image quality that clinicians can expect when using specific acquisition protocols and further predicting the expected quantitative image measurement performance for a particular clinical task. Clinicians need these tools given the fundamental tradeoff between CT image quality and radiation dose, and the complexity of the relationships between clinical task performance and CT acquisition parameters (2-6). In this manuscript we explore methods for predicting lung nodule volume measurement performance, which can provide clinicians with a direct estimate of expected CT image quality for specific acquisition protocols. While the methods were originally developed for estimating lung nodule volume measurement in the context of low dose CT lung cancer screening, the methods have broad applicability for informing the quality of lung nodule measurement in the routine clinical care setting.
CT image quality has historically relied on measuring a complex collection of image quality indicators, such as contrast, spatial resolution, image noise, and specific image artifacts. In addition numerous research articles have presented CT image quality metrics that correlate with general clinical task performance (7,8). While these methods can be useful, the complexity of interpretation of the results for a specific clinical task, such as for assessing small CT lung nodule volume measurement error, exceeds the expertise available at most clinical sites. Our goal here is to directly predict the statistical performance of an image-based clinical task if it were to be performed many times with a specified CT image acquisition system and a specific image measurement algorithm. The approach we describe here is more useful than a general purpose image quality index where the goal is to achieve a general correlation with CT image quality and clinical task performance. Additionally, producing a direct performance prediction for a specific clinical task, such as CT lung nodule volume measurement bias and precision, is easier to evaluate and use as it supports direct comparison of observed and predicted measurement performance.
Methods
The measurement prediction approach we implemented for this study has three principal computational steps consisting of an image acquisition model, a target object model, and a computational image analysis algorithm. First, we estimate fundamental CT image quality characteristics for a CT scanner and image acquisition protocol by analyzing a CT scan of a reference object with well-known and highly stable geometric and material properties. This results in a first order mathematical approximation, or model, of the CT image acquisition system. Next, we combine the acquisition system model with a set of virtual models of nodules to produce simulated images that exhibit variation in image noise, nodule position, and other characteristics, which is consistent with what would happen in real world CT scans. Finally, a segmentation is performed on the nodules in the simulated CT images using a standard CT lung nodule volume segmentation algorithm, yielding a set of lung nodule volume measurements. The resulting CT lung nodule volume measurements are then statistically analyzed, resulting in estimates of the expected volume measurement precision and bias of the target CT image acquisition and lung nodule volume measurement system.
We are not the first research group to explore this type of approach to estimating the quantitative measurement performance of a CT scanner and acquisition protocol (9). Funaki et al. demonstrated in 2012 a similar approach as reported here to predicting volumetric measurement performance (10) where volume measurement bias was predicted, but stopped short of also predicting volume measurement precision. This work, which was developed independently, extends this approach to predict both volume measurement bias and precision and uses an easy to manufacture geometric object (a concentric cylinder) and sophisticated optimization algorithm to arrive at improved prediction performance.
System modeling
We estimate a fundamental set of CT image quality characteristics to generate the image acquisition model used in this study. This includes methods for characterizing 3D resolution, 3D sampling rate, CT linearity, and image noise. The 3D sampling rate was represented as the linear distance between voxels in the X, Y, and Z dimensions, expressed in millimeters. A 3D Gaussian point spread function (PSF) specified as sigma values in millimeters for each 3D dimension (σx, σy, σz) was used to represent the 3D resolution of the image acquisition system. CT linearity specified the amount of bias from their expected Hounsfield units (HU) values for a set of homogeneous materials, taking care to avoid influence of partial volume artifact. The standard deviation of HU values for a specific homogeneous material was used to represent image noise.
The object model considered for this study was a solid lung nodule represented as a perfect sphere with a specific position and radius. The sphere model also contained values representing the HU densities of the sphere and the background material surrounding the sphere.
To simulate CT image formation, we first created a blank 3D image with the same 3D spacing used by the chest phantom protocol. Next the target object model was rasterized (i.e., scan converted) into the image volume with the given position (p), orientation vector (v), and spacing (s). Following this we convolved the 3D PSF with the target object model representation, including expected HU nodule foreground and background densities, to produce a simulated image with partial volume and sampling artifacts. The precise location of the sphere model within the 3D rectilinear grid was allowed to slightly change randomly each time a simulated image was generated, which is similar to what occurs in real world CT scanning. Finally, additive white Gaussian noise was randomly added to the image to simulate image noise. Figure 1 shows the image formation process for a simulated nodule.
The third and final sub-system modeled with this method was the software analysis algorithm. A 3D segmentation algorithm was run on the simulated nodule images using a constant threshold set halfway between the HU values representing the expected background and foreground materials. A polygonal closed surface was obtained using a 3D marching cubes algorithm and was quantitatively measured to arrive at the volume of the simulated nodule. Segmentation and measurement calculations were performed using algorithms from the Insight Segmentation and Registration Toolkit (ITK) (11).
Performance prediction methods
To determine the fundamental image characteristics for the image acquisition model, a reference object was necessary. We CT scanned and analyzed rolls of 3M Scotch Magic™ tape to build a mathematical 3D image acquisition model. This approach is advantageous as tape is widely available and inexpensive, and exhibits both the geometry and material properties that are important for estimating the performance of CT lung nodule volumetry. To obtain the needed study data, 3 new rolls of 3M 3/4 × 1000 Inch Scotch Magic™ tape were CT scanned on a GE LightSpeed VCT scanner using a routine chest imaging protocol. The acquired CT scotch tape data was then reconstructed into CT datasets of varying slice thicknesses (0.65, 1.25, and 2.5 mm). Slice spacing was set to be equal to slice thickness for all CT data obtained during this study. Figure 2 shows the placement of the scotch tape on the CT scanner table and the alignment of one roll of tape with CT scanner iso-center.

Automated image quality assessment software independently analyzed each of the three CT tape scan datasets. The system searched for and detected the rolls of scotch tape using a combination of size, shape, and HU density characteristics. For each detected roll of tape, the algorithm identified the tape’s core inner cylindrical ring region, making sure not to include a central plastic structure. A multi-pass optimization algorithm (13) determined the best fit values for the 3D position, 3D orientation, and 3D Gaussian PSF sigmas (σx, σy, σz) of the actual scotch tape scan data, where σx = σy. Use of one sigma value to represent the in-plane resolution of the acquisition system is common for CT calibration and reasonable considering that virtually all thoracic CT scans currently use helical scanning. It is important to note that the cylindrical shape of the tape and its orientation as it lays flat on the CT table were specifically chosen to support the quantitative estimation of in-plane resolution (σx = σy), and Z resolution (σz).
The optimization process is illustrated in Figure 3. Rolls of scotch tape are automatically detected by a geometrical discriminator that is constrained by the shape, intensity and size of the scotch tape. The inner ring of the scotch tape has a diameter of 34.62 mm with a height of 12.7 mm. The roll of tape has an approximate density of 115 HU. The discriminator computes an estimate of the position coordinate {p} and orientation vector {v} for each roll of scotch tape. Based on the initial position, an estimate of the densities of the tape as well as that of the air inside is obtained by taking the mean of the object densities within the core materials, taking care to avoid partial volume voxels at the boundary. An initial estimate of the Gaussian sigmas {σx, σy, σz} used to approximate the PSF is initialized as the three-dimensional image spacing.
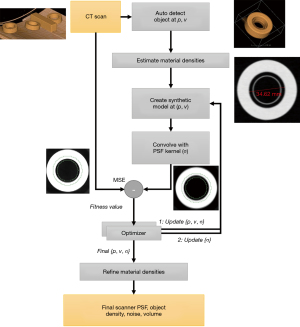
From the initial estimates, an optimizer is used to minimize the error between a simulated model of the scotch tape and the observed CT image of the scotch tape. The optimizer minimizes the following 8 variates {p, v, σ}: 3 positional variates, 3 orientation variates, 2 for the PSF (comprised of in-plane and out-of-plane resolutions) via an iterative process that starts from the initial estimates described above. The optimization is done in a region about the inner ring of the scotch tape, as illustrated via the green concentric circles in Figure 3. At each iteration, a simulated model of the scotch tape is generated by simulating the image formation process. This is done by inserting a scotch tape model into the image volume centered at the position, {p}, and oriented along the vector, {v}. The rasterization of the scotch tape into the image volume of spacing, {s}, is done while accounting for partial volume voxels, i.e., a voxel which contains 50% of the object (tape) and 50% of background (air) will have an intensity that’s half way between tape and air. This is followed by convolving the volume with a 3D PSF kernel. Since the 3D PSF is approximated as a Gaussian kernel, this is efficiently done via convolution with an finite impulse response filter. This blurs the image by using a separable convolution with discrete Gaussian kernels; with the kernel operator as described by Lindberg (14). The kernel is truncated to a width of 30 voxels away from the central voxel along each axis for computational speed. The simulated image goes through the image formation process but is devoid of noise. The difference between the simulated and observed CT image of the section of the tape should be mostly comprised of noise when the optimizer converges. The difference calculation is limited to a region about the inner ring capturing the transition between the tape and air as illustrated in Figure 3, which shows the region between the two green concentric circles. This section is automatically computed given the geometry of the tape and based on the estimated position and orientation at the end of the first optimization pass.
The root mean square error (RMSE) difference between the simulated and observed is minimized using a Simplex Optimizer. The optimization happens in two passes. In the first pass, the position, orientation and resolution are minimized jointly. In the second pass, the resolution alone is minimized. Multiple restarts of the optimizer are used to potentially avoid getting trapped in local minima. At the end of the optimization, the variates that result in the least difference between the observed and simulated image are stored. This provides an estimate of the 3D PSF. An added benefit of this approach is that the RMSE, after local noise has been subtracted, can provide quantitative information on the quality of the 3D PSF estimate. Higher final RMSE values above what can be accounted for by local image noise indicates a lower quality 3D PSF estimate.
Measurement of the densities of tape and air are used to estimate the material CT HU values and noise. This is achieved by calculating mean HU densities for both the air region at the center of the scotch tape core and the scotch tape material. These measurements are taken with care to avoid the influence of partial volume artifacts using knowledge of the 3D PSF. The CT HU bias is then calculated as the difference between the mean HU and the expected HU for both tape and air materials. Image noise is calculated by measuring standard deviation for the air and tape materials, using the same identified region as the region used for measuring mean HU values. Although other CT image quality characteristics, such as levels of edge enhancement, were calculated from each tape scan, they were not used in this analysis.
The study utilized three geometric nodule models for representing Teflon spheres, each with a different diameter (4.0, 6.0, and 8.0 mm). Given that the objective was to predict volume measurement accuracy of Teflon spheres packed within low density foam, the CT values of the sphere and background were fixed to the expected values for Teflon (HU =870) and foam (HU =−973) materials. While the study computed bias values for air and tape materials at three different locations from the iso-center, these values were not utilized. Thus, a zero CT bias for both materials was used. Accounting for CT value bias, which differed from expected by less than 20 HU, would have had a negligible impact on the reported results and would have required a significant amount of additional effort. Each sphere’s distance from iso-center would need to be calculated and a model of how the expected CT value bias changed as a function of distance from iso-center would have been needed to be calculated for each material.
For each of three CT slice thicknesses and nodule model diameters, simulated images were automatically generated, segmented, and quantitatively measured volumetrically. Mean, standard deviation, and coefficient of variation (CV) statistics were calculated using the volume measurements for each nodule size and slice thickness pair, establishing the measurement performance prediction. Interpolation between the simulated nodule diameter values was used for comparison against the real Teflon sphere diameters. The mean and CV values for each of the three sphere model diameters was measured using 150 generated 3D CT images.
Observed performance methods
To obtain quantitative volumetric measurement performance of an independent volume measurement algorithm we first CT scanned an anthropomorphic chest phantom containing Teflon spheres embedded in foam (diameters =4.76, 6.36, and 7.94 mm). This anthropomorphic chest phantom was scanned 10 times on the same GE VCT scanner and CT image acquisition protocol as the CT scan of the scotch tape rolls. AJ independently developed a nodule measurement algorithm (15) that used a constant threshold to volumetrically measure the Teflon spheres acquired within the 30 (3 reconstructions per scan) repeat CT image acquisitions. AJ was blinded to the prediction results prior to submitting his independent algorithm results. Although the AJ algorithm used an identical HU threshold as the prediction algorithm for generating a nodule surface, the algorithm did not use ITK and used different code for thresholding and calculating the volume of the Teflon spheres. The resulting volume measurements were used to calculate mean, standard deviation, and CV statistics and established the observed volume measurement performance.
Results
Table 1 shows both the predicted and observed volume measurement statistics for the 3 Teflon sphere diameters and three CT slice thicknesses used in the study. Predicted mean and CV statistics were calculated on results run on simulated images as described in the methods section and observed mean and CV statistics were calculated from the volume measurements reported using AJ’s segmentation method. Each pair of values in the table represents the mean and CV percentage of the volumetric measurements.
Table 1
| Slice thickness | Sphere diameter | |||||||
|---|---|---|---|---|---|---|---|---|
| 4.76 mm (56.5 mm3) | 6.36 mm (134.7 mm3) | 7.94 mm (262.1 mm3) | ||||||
| Predicted | Observed | Predicted | Observed | Predicted | Observed | |||
| 0.625 mm | 44.3, 0.91 | 48.2, 1.17 | 110.4, 0.51 | 124.1, 0.47 | 219.9, 0.29 | 250.1, 0.34 | ||
| 1.25 mm | 42.1, 0.98 | 47.6, 1.35 | 106.9, 0.56 | 123.1, 0.61 | 214.8, 0.32 | 248.8, 0.41 | ||
| 2.5 mm | 23.9, 9.53 | 36.8,12.50 | 77.6, 3.84 | 110.5, 3.20 | 173.0, 1.57 | 233.9, 1.32 | ||
Each pair of values represents the mean volume (mm3) and the CV (%) of the volumetric measurements. Reused with the permission from Ref. (12). CV, coefficient of variation.
Figures 4,5 show predicted versus observed volumetric measurement mean bias and precision performance, respectively.
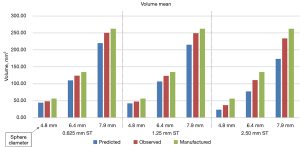
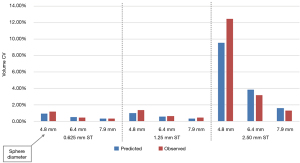
The predicted and observed volume mean for all slice thicknesses was found to be 28% and 13% lower on average than the manufactured sphere volume, respectively. When restricted to 0.625 and 1.25 mm slice thickness scans, which are recommended for small lung nodule volume measurement, the predicted and observed volume mean measurements were found to be 20% and 9% lower than manufactured. We also found that the difference between predicted and observed volume CV was less than 1.0% for all nodule sizes and slice thicknesses except when measuring a 4.8 mm diameter sphere using 2.5 mm slice thickness.
Discussion
We have provided data highlighting several important capabilities and advancements for CT quantitative imaging. First, is that prediction of the CT measurement performance statistics for a specific clinical task can be performed by a simple image generation simulation engine that uses a small set of fundamental CT image characteristics. Similarly, modern CT scanners routinely provide radiation dose estimates (16) for healthcare providers, which also use modeling and assumptions.
In this study we calculated predictions of sphere volume measurements that were consistent with independently measured volumetric sphere measurements, using an anthropomorphic CT chest phantom. The approach expressed predicted performance for a specific quantitative clinical task in direct and commonly used volumetric measurement performance statistical metrics (bias and CV). This is of particular importance as physicians need to understand expected scanner and software performance in clinically meaningful terms. As oncologic imaging is highly dependent on the ability to measure change in volume over time as either a measure of response or progression (17), the ability to predict the CV in a given measurement will be a critical piece of information in terms of deciding whether change is genuine or instead due to measurement error. The type of information provided here can form the basis for understanding how much change will be necessary in order to decide if it is real, and then it also provides a basis for determining how long a delay will be necessary between scans in order to anticipate the extent of change predicted so as to overcome measurement variability. This is a critical step in terms of individualizing the approach to obtaining follow-up scans.
A second important finding is that inexpensive and easy to obtain reference objects, in this case 3 rolls of a commonly available brand of scotch tape, can be used to estimate the fundamental performance of a medical image acquisition system. Overall, this study shows that a small and fundamental set of image quality metrics obtained by scanning and analyzing a low-cost reference object can be used to predict the expected quantitative performance of a medical scanning and measurement system. Despite the ultra-low cost of these reference objects, we found that analysis of them using advanced image processing and analysis methods, as described above, can provide highly accurate and useful image quality characteristics (e.g., 3D spatial resolution).
We were not the first to demonstrate the potential of this type of approach to estimating small lung nodule volume measurement performance. Funaki et al., implemented a similar approach in 2012 and also provided predicted performance of volumetric measurement of small spheres (10). However, they only went as far as predicting the mean volume of spheres and obtained lower prediction performance than reported here. To our knowledge the prediction performance reported here is the first report of a calibration phantom-based method predicting both the volumetric bias and precision of a CT scanner, acquisition protocol, and a general class of volumetric measurement software.
An underestimation of mean volumetric measurement values with respect to the manufactured volume was observed, particularly for the thickest slice thickness used. An increasing negative volume measurement bias is expected when a small reference object is CT scanned with larger slice thicknesses and both the predicted and observed performance showed this in Figure 4. As shown by Mendonça et al. (18), a negative edge localization bias will be present when a convex edge is convolved with a point spread function. This is a fundamental property of imaging systems and demonstrates an alignment of computer vision modeling theory and experimentally derived results. Our volumetric measurement bias results are also consistent with independent results reported by Prionas et al. (19).
Increasing volume measurement bias is also due to greater partial volume artifact influence across the surface area of small reference objects. A greater influence of partial volume artifact on small reference objects is also responsible for an increasing CV when thicker slice thicknesses are used. Another factor which may have contributed to a negative volume measurement bias with thicker slices is that the slice sensitivity profile of the thickest slice thickness used (2.5 mm) departs further from a Gaussian profile. A Gaussian 3D PSF was used for representing the 3D resolution of the acquisition system. More advanced methods for modeling the PSF along the Z axis has potential to improve our prediction performance for CT slice thicknesses larger than 1.25 mm as scanner manufacturers often combine CT slices to generate thick slices. As a result, a Gaussian PSF model may not be the best choice for thick CT slices. However, in the setting of predicting volumetric measurement performance for lung cancer screening studies, better modeling of thicker slices is not a priority as thin, ≤1.25 mm slice thickness is recommended by numerous screening guidance documents (20,21).
The analysis of the scotch tape scans resulted in three independent estimates of the 3D PSF at different distances from scanner iso-center. Spatial resolution at a location within a CT scan can be efficiently expressed as the volume of the 3D PSF ellipsoid. As expected, we observed a loss of 3D spatial resolution as a function of distance from iso-center for all scans. For example, the 3D PSF ellipsoid volume measurements for a 0.625 mm slice thickness scan were 0.370, 0.502, and 0.620 mm3 at distances of 38, 93, and 177 mm from scanner iso-center, respectively. A future improvement to our prediction method is to leverage the spatially varying 3D PSF information when creating the simulated sphere images. This would better model CT scanners and image acquisition protocols that have a large loss of resolution as a function of distance to iso-center.
Another factor is that the scotch tape reference objects were not surrounded by a water equivalent mass representing a human chest. This resulted in an underestimation of the image noise present in the anthropomorphic phantom scan when predicting volumetric measurement performance, which could have contributed toward volume bias and imprecision. These factors indicate that improved modeling of the 3 sub-systems will likely improve the measurement prediction performance in future studies. In addition, a more advanced CT image noise model, such as the noise power spectra, and a better match of the computational processing algorithms used for the predicted and observed segmentation algorithms are some of the steps that will likely be needed to achieve improved task performance prediction values.
Another limitation of the current study is that we only evaluated a simple sphere model for this study. Adding elliptical and other shapes would have added much more complexity to the study and potentially made the results harder to gauge because the simulation would have needed to know the orientation of the ellipsoids (or other shapes) to model them correctly. Estimating object orientation from acquired images would have introduced another source of error in the study which likely would have made the results more difficult to interpret. Secondly, the only prior published paper performing similar work also used spheres and it is advantageous to be able to compare our reported performance to these previously published results. However, further evaluation of this approach should be extended to more complex nodule and patient presentations, potentially using spheres, ellipsoids, and more complex nodule models. As we conduct further studies, we plan to determine how much more complexity to add to the modeling methods to better model a wide range of medical image acquisition systems, patient presentations, and image analysis algorithms. While the closeness of our predicted to actual volume measures are important indicators of the robustness of our technique, these are likely to vary based on assumptions made for a given software. However, the precision of volume measurement, expressed here as a CV, is a more meaningful measure as this will be more important in estimating change over time, which is not dependent on bias in the absolute volume estimate. Here we see even closer agreement between actual and predicted measures.
The choice to not use an edge enhancing reconstruction kernel during CT image acquisition had several motivations. First, is that edge enhancement can significantly over-estimate the HU density at the edge of objects and greatly bias the ability to estimate the in-plane resolution of the CT acquisition since it is computed using edge intensities. Third, the application of edge-enhancement is only performed in-plane and not along the Z dimension and is generally avoided when performing precise quantitative CT measurements.
We used spheres manufactured out of Teflon and modeled the spheres during image simulation using a Teflon HU density. While the HU density of Teflon is significantly higher than real lung nodules in the clinical setting, we are not aware of any advantage this choice of material would provide to predicting volumetric measurement bias and precision. A future study using a range of materials would help determine the potential for higher density materials to bias volume measurement prediction performance in these types of studies.
Better methods for validating prediction performance are also needed. The CT acquisition of more than 10 repeat CT scans for each sphere size and slice thickness pair would have improved our ability to measure observed volume measurement performance. However, performing large numbers of CT scans is challenging to achieve in a clinical setting as the increased CT acquisition time is difficult to obtain at most clinical institutions.
Despite these limitations, this study demonstrates that obtaining fundamental CT image quality characteristics and using this information to predict quantitative CT measurement performance has potential to inform clinicians. A naïve approach to performance prediction likely would have made the assumption that 1.25 mm slice thickness scanning would result in much higher volumetric measurement CV than a 0.625 mm slice thickness CT scan. However, our image quality analysis algorithm found that the estimated Z resolutions of these very different CT slice thicknesses was in actually fairly similar. Because our simulation approach used scotch tape measured resolution estimates, our prediction performance more closely matched the observed performance. Had we used a Z resolution estimate based on the requested slice thickness within the DICOM header, our volumetric measurement prediction performance would not have performed as well as was reported here. Our approach, which estimates and uses fundamental image quality metrics, has potential to provide improved quantitative measurement prediction performance and resilience to varying many other CT image acquisition parameters beyond CT slice thickness.
The methods described here can also potentially support many other clinical tasks and other modalities beyond quantitative CT volumetry. One highly useful extension of this work has the potential to address a very important clinical imaging responsibility which is in need of better quantitative tools. Specifically, these methods have the potential to predict and optimize both radiation exposure and quantitative CT image measurement performance, which can be difficult to optimize for a specific patient circumstance.
Conclusions
This study demonstrated for the first time that a fully automated calibration phantom-based analysis combined with CT image formation simulation methods can be used to predict CT volume measurement bias and precision for small 5 to 8 mm diameter solid objects. In addition, this study demonstrated that a reference object need not be expensive or difficult to acquire. This study used very low-cost reference objects (3 rolls of Scotch Magic™ tape) and achieved useful spatial resolution and other key CT image quality measurements. This approach is also notable in that it directly predicts the statistical performance of an important clinical task metric, namely the volume measurement of small solid lung nodules. The approach demonstrates a new and more effective method for predicting task specific, clinically relevant measurement performance using advanced and fully automated image analysis techniques and low-cost reference objects.
Acknowledgments
Funding: None.
Footnote
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://qims.amegroups.com/article/view/10.21037/qims-22-320/coif). Ricardo Avila is the CEO and owns stock in Accumetra. Accumetra also holds and submits patents in the area of CT image quality. He is also the owner of Paraxial, LLC which develops imaging software and other technologies. Ricardo Avila’s wife (Lisa Avila) is the CEO of Kitware which also develops imaging software and other technologies. Karthik Krishnan is an independent consultant of Accumetra, LLC. NO collaborates with QIBA as a statistical consultant through a contract between her institution and RSNA. AJ received a 2-year $100k grant from the Prevent Cancer Foundation for a project to model factors influencing nodule measurement uncertainty. The grant was paid to my institution and ended in Jan 2021. This is not directly related to this manuscript other than the overarching theme of trying to make better measurements. DY is a named inventor on a number of patents and patent applications related to the evaluation of chest diseases including measurements of chest nodules. He has received financial compensation for the licensing of these patents. In addition, he is a consultant and co-owner of Accumetra, a private company developing tools to improve the quality of CT imaging. He is on the advisory board and owns equity in HeartLung, a company that develops software related to CT scans of the chest. He is on the medical advisory board of Median Technology that is developing technology related to analyzing pulmonary nodules and is on the medical advisory board of Carestream, a company that develops radiography equipment and has consulted for Genentech, AstraZeneca and Pfizer. The other author has no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. Ethical approval was not needed in this study because all data were obtained using calibration phantoms and reference objects.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- ACR. ACR Statement on FDA Radiation Reduction Program. Available online: https://www.acr.org/About-Us/Media-Center/Position-Statements/Position-Statements-Folder/ACR-Statement-on-FDA-Radiation-Reduction-Program. Position Statement, 2011.
- Ravenel JG, Leue WM, Nietert PJ, Miller JV, Taylor KK, Silvestri GA. Pulmonary nodule volume: effects of reconstruction parameters on automated measurements--a phantom study. Radiology 2008;247:400-8. [Crossref] [PubMed]
- Das M, Ley-Zaporozhan J, Gietema HA, Czech A, Mühlenbruch G, Mahnken AH, Katoh M, Bakai A, Salganicoff M, Diederich S, Prokop M, Kauczor HU, Günther RW, Wildberger JE. Accuracy of automated volumetry of pulmonary nodules across different multislice CT scanners. Eur Radiol 2007;17:1979-84. [Crossref] [PubMed]
- Petrou M, Quint LE, Nan B, Baker LH. Pulmonary nodule volumetric measurement variability as a function of CT slice thickness and nodule morphology. AJR Am J Roentgenol 2007;188:306-12. [Crossref] [PubMed]
- Wielpütz MO, Lederlin M, Wroblewski J, Dinkel J, Eichinger M, Biederer J, Kauczor HU, Puderbach M. CT volumetry of artificial pulmonary nodules using an ex vivo lung phantom: influence of exposure parameters and iterative reconstruction on reproducibility. Eur J Radiol 2013;82:1577-83. [Crossref] [PubMed]
- Wang Y, de Bock GH, van Klaveren RJ, van Ooyen P, Tukker W, Zhao Y, Dorrius MD, Proença RV, Post WJ, Oudkerk M. Volumetric measurement of pulmonary nodules at low-dose chest CT: effect of reconstruction setting on measurement variability. Eur Radiol 2010;20:1180-7. [Crossref] [PubMed]
- Goldman LW. Principles of CT: radiation dose and image quality. J Nucl Med Technol 2007;35:213-25; quiz 226-8. [Crossref] [PubMed]
- Christianson O, Chen JJ, Yang Z, Saiprasad G, Dima A, Filliben JJ, Peskin A, Trimble C, Siegel EL, Samei E. An Improved Index of Image Quality for Task-based Performance of CT Iterative Reconstruction across Three Commercial Implementations. Radiology 2015;275:725-34. [Crossref] [PubMed]
- Ohkubo M, Wada S, Ida S, Kunii M, Kayugawa A, Matsumoto T, Nishizawa K, Murao K. Determination of point spread function in computed tomography accompanied with verification. Med Phys 2009;36:2089-97. [Crossref] [PubMed]
- Funaki A, Ohkubo M, Wada S, Murao K, Matsumoto T, Niizuma S. Application of CT-PSF-based computer-simulated lung nodules for evaluating the accuracy of computer-aided volumetry. Radiol Phys Technol 2012;5:166-71. [Crossref] [PubMed]
- McCormick M, Liu X, Jomier J, Marion C, Ibanez L. ITK: enabling reproducible research and open science. Front Neuroinform 2014;8:13. [Crossref] [PubMed]
- Avila RS, Jirapatnakul A, Subramaniam R, Yankelevitz D. A new method for predicting CT lung nodule volume measurement performance. Proc. SPIE 10134, Medical Imaging 2017 Computer-Aided Diagnosis 2017;101343Y:3.
- Kinahan PE, Byrd DW, Helba B, Wangerin KA, Liu X, Levy JR, Allberg KC, Krishnan K, Avila RS. Simultaneous Estimation of Bias and Resolution in PET Images With a Long-Lived "Pocket" Phantom System. Tomography 2018;4:33-41. [Crossref] [PubMed]
- Lindeberg T. Discrete scale-space theory and the scale-space primal sketch". PhD thesis, Royal Institute of Technology, S-10044. Stockholm, Sweden; May 1991.
- Reeves AP, Chan AB, Yankelevitz DF, Henschke CI, Kressler B, Kostis WJ. On measuring the change in size of pulmonary nodules. IEEE Trans Med Imaging 2006;25:435-50. [Crossref] [PubMed]
- Strauss KJ, McKenney SE, Brady SL. Improved Estimates of Trunk and Head CT Radiation Dose: Development of Size-Specific Dose Estimate. J Am Coll Radiol 2020;17:560-2. [Crossref] [PubMed]
- Lee JH, Lee HY, Ahn MJ, Park K, Ahn JS, Sun JM, Lee KS. Volume-based growth tumor kinetics as a prognostic biomarker for patients with EGFR mutant lung adenocarcinoma undergoing EGFR tyrosine kinase inhibitor therapy: a case control study. Cancer Imaging 2016;16:5. [Crossref] [PubMed]
- Mendonça PRS, Padfield D, Miller J, Turek M. Bias in the Localization of Curved Edges. In: Pajdla T, Matas J (eds). Computer Vision - ECCV 2004. Lecture Notes in Computer Science, Vol 3022. Berlin, Heidelberg: Springer; 2004.
- Prionas ND, Ray S, Boone JM. Volume assessment accuracy in computed tomography: a phantom study. J Appl Clin Med Phys 2010;11:3037. [Crossref] [PubMed]
- Mulshine JL, Gierada DS, Armato SG 3rd, Avila RS, Yankelevitz DF, Kazerooni EA, McNitt-Gray MF, Buckler AJ, Sullivan DC. Role of the Quantitative Imaging Biomarker Alliance in optimizing CT for the evaluation of lung cancer screen-detected nodules. J Am Coll Radiol 2015;12:390-5. [Crossref] [PubMed]
- Yankelevitz DF, Yip R, Smith JP, Liang M, Liu Y, Xu DM, Salvatore MM, Wolf AS, Flores RM, Henschke CIInternational Early Lung Cancer Action Program Investigators Group. CT Screening for Lung Cancer: Nonsolid Nodules in Baseline and Annual Repeat Rounds. Radiology 2015;277:555-64. [Crossref] [PubMed]



