
Improvements of the Tada formula in estimating the intracerebral hemorrhage volume based on computed tomography
Introduction
Intracerebral hemorrhage (ICH) refers to hemorrhage caused by rupture of blood vessels in the brain parenchyma and the subsequent entry of blood into the ventricles (1,2). ICH is the most severe type of stroke (3), and the number of hospital admissions for ICH has increased worldwide (4). According to relevant statistics, 30% of survivors of ICH have various degrees of sequelae (5,6). The disease can have a serious impact on the patient’s quality of life, and early accurate assessment of the condition and timely treatment are of great importance to patient prognosis. The amount of bleeding is a convenient, reliable, and independent predictor of the prognosis for these patients (7-9). The Tada formula, also known as the π/6ABC formula, was developed for calculating hematoma volume. For the convenience of clinical practice, the Tada formula is simplified and modified into 1/2ABC, which is widely used. However, 1/2ABC is relatively accurate when measuring hematoma volume with a regular hemorrhage shape, but when it is irregularly shaped—as is typically the case—1/2ABC will overestimate the size of the hematoma volume. Therefore, researchers reported that 1/3ABC is better suited for calculating irregular hematomas. Although 1/3ABC is more accurate than 1/2ABC when the shape of the hematoma is irregular, the volume of the hematoma may be underestimated by 1/3ABC (10). Other modifications have also been described, such as 1/2SH, 2/3SH, and 2.5/6ABC (11); however, modifications have not been widely used in clinical practice and still need further study. Although the Tada formula can be used to quickly estimate the hematoma volume, the calculation error by the Tada formula will affect clinical decision-making, such as prognostication or surgery planning. Computer-aided volume measuring tools are gradually being developed, including 3D image reconstruction software and some artificial intelligence software. 3D image reconstruction software, such as FireVoxel, Analyze and 3Dslicer, have high accuracy in measuring hematoma by manually delineating the segmented hematoma on each CT slice and can be used as the gold standard for measuring hematoma volume. Artificial intelligence software developed by deep machine learning algorithms can automatically segment hematomas, greatly reducing hematoma segmentation time. Unfortunately, 3D reconstruction software needs to manually delineate the hematoma area on each CT slice, which is time-consuming and not suitable for emergency ICH hematoma volume measurement. Artifacts of CT images caused by metal, motion, and noise will also greatly reduce the accuracy of automatic segmentation hematoma algorithms while using artificial intelligence software to measure the ICH hematoma volume. In addition, these software programs are not integrated with the hospital imaging system and cannot directly obtain the original format of CT images. Hence, it is essential to investigate a simpler, more accurate, and more reliable approach for calculating the ICH volume. FireVoxel is a free medical image texture analysis and processing platform (https://wp.nyu.edu/FireVoxel) and can be used for 3D image reconstruction, visual analysis, and volume measurement (12).
Using FireVoxel to calculate the volume of hematoma mainly depends on the manually delineated hematoma area, and there is no absolute gold standard for the calculation of these hematoma volumes. To demonstrate the high accuracy of FireVoxel in measuring the volume, the predetermined volume of water was injected into balls of different shapes, and the water volume was calculated by delineating the ball CT images using FireVoxel, which was similar to the hematoma volume calculation. The measurement value of FireVoxel was set as the gold standard. We then explored the correlation between the volume measured by the Tada formula (1/2ABC for regular shape and Tada 1/3ABC for irregular shape) and FireVoxel by polynomial fitting to produce a corrected Tada formula (C-Tada formula) for measuring the ICH volume with sufficient convenience and accuracy. We present this article in accordance with the GRRAS reporting checklist (available at https://qims.amegroups.com/article/view/10.21037/qims-22-1084/rc).
Methods
Experimental materials
Given that the ICHs are typically of different shapes, 15 empty balls were put into boiling water to be squeezed with external force into irregular shapes to simulate ICHs. Then, water with an accurately measured volume was injected to completely fill each ball.
Clinical materials
A total of 329 patients (age 12–90 years) with spontaneous ICHs of different shapes were enrolled from July 2017 to March 2019. The imaging data of 245 patients admitted to Tianjin Medical University General Hospital were set as a training dataset, and the imaging data of 84 patients admitted to the Affiliated Hospital of Xuzhou Medical University were set as a test dataset. Inclusion criteria: (I) differing degrees of clinical symptoms; (II) brain CT examination findings available within 24 hours of symptom onset. Exclusion criteria: (I) traumatic ICH; (II) hemorrhage secondary to aneurism or arteriovenous malformation; (III) intraparenchymal tumor hemorrhage; (IV) epidural or subdural hematoma.
Imaging study
The imaging data of 15 ball and 329 patient brain CT scans (64-slice, GE Healthcare, Chicago, IL, USA) were obtained through the hospital picture archiving and communication system (PACS) and saved in Digital Imaging and Communications in Medicine (DICOM) format. The section thickness of the ball and brain CTs were 5 mm (with no gap), the window width was 80 HU, and the window level was 35 HU. Additionally, basic information affecting the images, including the location, shape and level of the hematoma, was recorded. The CT images were reviewed independently by two experienced neurosurgeons (Dr. Tian and Dr. Gao) blinded to the data. Ball and hematoma volumes were calculated as follows: (I) FireVoxel method: FireVoxel image processing software was used to import the CT image data (in DICOM format). Then, the “load 3D” command was clicked, and after selecting the parameters (1,024×485), the areas of the hematoma in each slice were outlined by hand. Finally, by clicking “ROI Stats 3D”, the results were exported; (II) Tada formula method: The Formula V = 1/2×A×B×C (for regular shape) and 1/3×A×B×C (for irregular shape), where A (mm) is the maximum hematoma length, B (mm) is the maximum width perpendicular to A (mm) determined on the slice of maximal area, and C is the depth of the hematoma. The interrater variability of using FireVoxel and Tada formula to measure the volume of ICH and the interrater agreements on categorizing the shapes of hematoma were estimated by two experienced neurosurgeons through 200 patient brain CT images. Although there was low interrater variability (Table S1) between the two experienced neurosurgeons in the volume measurement, the results of the hematoma volume calculation from the two neurosurgeons were averaged to reduce deviation. Although there was high interrater agreement on categorizing the shapes of hematoma (Table S2), cases of disagreement on hematoma shape reviewed by the two neurosurgeons (Dr. Tian and Dr. Gao) existed. In cases of disagreement, professor Jiang, who is an experienced neurosurgery expert, made a joint decision with the two neurosurgeons (Dr. Tian and Dr. Gao).
Ball and hematoma groups
Hematomas were also categorized into two groups using the 5-point category scale approach and the size of the largest ICH slice (13): (I) shape categories 1 and 2 (round, ellipsoid or oval) were designated as the regular group; (II) shape categories 3 to 5 (irregular, separated, multilobar, cauliflower shaped, etc.) were designated the irregular group (Figure S1). The ball images were grouped by shape: Regular group (n=5), Irregular group (n=10). Similarly, the hematoma images were also grouped by shape: regular group (training dataset, n=135; test dataset, n=42) and irregular group (training dataset, n=110; test dataset, n=42). The volumes of the hematomata were divided into groups according to the Fuji standard (14) and based on volume measured by the Tada formula: <30 mL group (training dataset, n=162; test dataset, n=39), 30–60 mL group (training dataset, n=65; test dataset, n=34), and >60 mL group (training dataset, n=18; test dataset, n=11).
Polynomial regression model
The polynomial regression model was employed to correct the Tada formula as follows:
where m is the degree of the polynomial, or the highest or the greatest power of variable x, xj denotes the j-th power of x, and wj is the coefficient of xj. If each wj and m are determined, one can obtain the corrected Tada value y by taking the value from the original Tada formula as input x.
Estimation of m and wj
To estimate m and wj, for (n+t) patients, we used the hematoma volume of patient i calculated by both the Tada formula and FireVoxel, denoted as xi and yi, respectively, and the pair (xi, yi), i=1,…,n to estimate each wj as follows:
The equations above can be rewritten in matrix form as follows:
where is the Vandermonde matrix and , according to the least-square estimation method. After some manipulations, the polynomial coefficient can be estimated according to the following formula:
where , and T denotes the transposition operation.
Suppose there are some other values ; we can employ these values to estimate the optimal m in Eq. [1]. Suppose m is fixed to, for example, 10; then, the polynomial coefficients can be estimated via Eq. [4] based on . Thus, for each , one can obtain an estimated based on the estimated polynomial coefficients, and the root mean square error (RMSE) can be calculated as follows:
Clearly, RMSEm depends on the degree of the polynomial, i.e., m. The value of m that minimizes RMSEm when m is in a particular range, for example, from 1 to 100, is the optimal value we need. However, the optimal m chosen in this way will yield very high-order polynomials that lead to overfitting. To overcome this issue, we only focus on low-order polynomials, i.e., polynomials of first order or second order. In most cases, the optimal criterion described in Eq. [5] yields low-order polynomials as well. In this way, the problem of overfitting can be overcome successfully.
Statistical analysis
Data were analyzed using Graph Pad v 8.0d (GraphPad Software, San Diego, CA, USA) or the SPSS 24.0 software package (SPSS Inc., Chicago, IL, USA). As most data were nonnormally distributed, measurement data are reported as the median with interquartile range (IQR) and were compared with the Wilcoxon matched-pairs signed rank-test for two related samples, the Kruskal-Wallis H test for multiple independent samples, and the Mann-Whitney U test for two independent samples. Correlation coefficients between volumetric assessments were performed with Spearman’s test. Interrater agreement and variability tests were analyzed using the Cohen kappa coefficient and intraclass correlation coefficient. Furthermore, the degree of agreement between each of the two methods (Tada formula and C-Tada formula) and FireVoxel (standard) was evaluated using Bland-Altman test plots. The effects of the different estimation methods on hematoma volume and the percentage deviations are shown using box plots. A value of P<0.05 was considered statistically significant.
Ethical statement
The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). This study was approved by the Institutional Ethics Committee of Tianjin Medical University General Hospital, and all participants provided written informed consent.
Results
The volume measured by FireVoxel can be set as the reference standard
Relative to the volume of the premeasured water in the balls (Figure 1A,1B), the median volumes of the actual water content (standard), FireVoxel estimation and Tada formula estimation were 23.00 mL (IQR, 19.00 mL), 24.90 mL (IQR, 18.50 mL), and 28.50 mL (IQR, 13.65 mL), respectively. There were significant differences among the actual volume, the FireVoxel-estimated volume and Tada formula-estimated volumes (P=0.007) (Figure 1C). The percentage deviation in the volume calculated by FireVoxel (median, 4.23%; IQR, 14.80%) was significantly lower than that calculated by the Tada formula (median, 14.64%; IQR, 59.07%) (P=0.041) (Figure 1D). Correlation (Spearman’s) coefficients for water volume measured by the FireVoxel and Tada formula versus absolute amount of water volume were 0.999 and 0.971, respectively (Figure 1E,1F). These results demonstrate that the measurements obtained by FireVoxel can be set as the standard to derive the C-Tada formula.
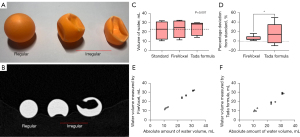
The accuracy of the Tada formula is influenced by the shape and volume of the hematoma
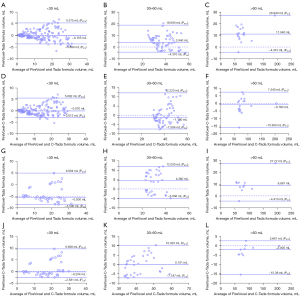
The hematoma volume was measured by the Tada formula and FireVoxel (Figure 2A-2K). The hematoma volume measured by Tada1/2ABC was significantly greater than that calculated by FireVoxel for the Regular group (P<0.001), and the opposite result was obtained in the irregular group (P<0.001). In addition, the hematoma volume calculated by FireVoxel was significantly different from that calculated by the Tada formula for each group divided by volume (<30 mL: P=0.021; 30–60 mL: P<0.001; >60 mL: P<0.001) (Table 1, Figure 3A,3B). Furthermore, the percentage deviation from FireVoxel was significantly different among the Regular and Irregular groups (P<0.001); similar results were obtained for the volume groups (P<0.001) (Table 2, Figure 3C,3D). These results suggest that the Tada formula should be corrected according to the shape and volume of the hematoma.
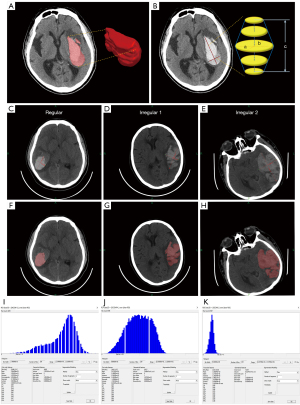
Table 1
| Volume of hematoma, mL | N | Method | Median | Maximum | Minimum | P75 | P25 | IQR | P value |
|---|---|---|---|---|---|---|---|---|---|
| Groups divided by shape | |||||||||
| Regular | 135 | FireVoxel | 12.06 | 60.02 | 0.43 | 23.20 | 4.30 | 18.90 | <0.001 |
| Tada formula | 12.82 | 64.43 | 0.33 | 25.77 | 4.18 | 21.59 | |||
| Irregular | 110 | FireVoxel | 31.85 | 204.9 | 2.32 | 48.16 | 19.35 | 28.81 | <0.001 |
| Tada formula | 26.27 | 178.0 | 2.16 | 39.85 | 17.53 | 22.32 | |||
| Groups divided by volume | |||||||||
| <30 mL | 162 | FireVoxel | 11.96 | 29.60 | 0.43 | 19.91 | 5.44 | 14.47 | 0.021 |
| Tada formula | 12.98 | 33.10 | 0.33 | 20.26 | 4.52 | 15.74 | |||
| 30–60 mL | 65 | FireVoxel | 37.20 | 59.10 | 30.07 | 46.90 | 30.07 | 16.83 | <0.001 |
| Tada formula | 36.07 | 59.10 | 18.05 | 40.83 | 18.05 | 22.78 | |||
| >60 mL | 18 | FireVoxel | 71.94 | 204.90 | 60.02 | 86.92 | 66.27 | 20.65 | <0.001 |
| Tada formula | 63.15 | 178.00 | 45.61 | 74.80 | 56.02 | 18.78 |
IQR, interquartile range.
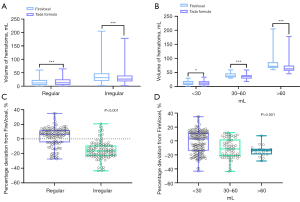
Table 2
| Percentage deviation from FireVoxel, % | N | Median | Maximum | Minimum | P75 | P25 | IQR | P value |
|---|---|---|---|---|---|---|---|---|
| Groups divided by shape | ||||||||
| Regular | 135 | 6.34 | 34.97 | −27.50 | 12.20 | −27.50 | 39.70 | <0.001 |
| Irregular | 110 | −16.43 | 20.85 | −43.58 | −8.97 | −23.04 | 14.07 | |
| Groups divided by shape | ||||||||
| <30 mL | 162 | 2.83 | 34.97 | −43.20 | 11.85 | −14.28 | 26.13 | <0.001 |
| 30–60 mL | 65 | −11.47 | 12.02 | −43.58 | 2.02 | −21.77 | 23.79 | |
| >60 mL | 18 | −19.33 | 7.35 | −28.69 | −11.28 | −19.33 | 8.05 |
IQR, interquartile range.
Measurement data corrected by polynomial fitting formulas show better consistency and greater accuracy
Using polynomial fitting to compare the volume measured by the Tada formula (Tada 1/2ABC for regular and Tada 1/3ABC for irregular) (X, mL) and FireVoxel (Y, mL), we obtained the following formulas:
Polynomial fitting formulas grouped by shape:
Regular:
Irregular:
Polynomial fitting formulas grouped by volume:
<30 mL:
30–60 mL:
60 mL:
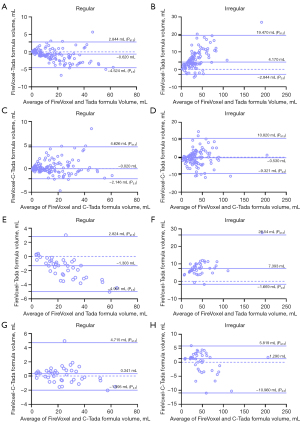
The correlation between the volume measured by the Tada formula and FireVoxel is shown in Figure 4. The hematoma volume measured by the Tada formula was corrected with polynomial fitting formulas (C-Tada formulas). Comparing the two methods (Tada and C-Tada) with Bland-Altman analysis against the standard (FireVoxel), the limits of agreement were tighter for the C-Tada formula for the shape groups in the training and test datasets (Tables 3,4). Specifically, the results in the training dataset were as follows: regular [−0.020 mL (−2.146 to 4.626 mL) versus −0.620 mL (−4.524 to 2.844 mL)] and irregular [−0.530 mL (−9.321 to 10.820 mL) versus 4.170 mL (−2.844 to 19.470 mL)] (Figure 5A-5D); the results in the test dataset were as follows: regular [0.341 mL (−1.995 to 4.715 mL) versus −1.303 mL (−4.961 to 2.824 mL)] and irregular [1.290 mL (−10.960 to 5.819 mL) versus 7.393 mL (−1.669 to 26.540 mL)] (Figure 5E-5H). At the same time, the limits of agreement of the two methods were also analyzed for the volume groups, which showed similar results to the shape groups (Tables 3,4). In the training dataset: <30 mL [−0.070 mL (−3.013 to 5.602 mL) versus −0.155 mL (−3.890 to 5.357 mL)], 30–60 mL [−1.190 mL (−7.506 to 12.220 mL) versus 3.940 mL (−4.370 to 18.690 mL)], and > 60 mL [−0.780 mL (−15.950 to 7.540 mL) versus 11.040 mL (−4.410 to 26.940 mL)] (Figure 6A-6F); in the test dataset: <30 mL [−0.204 mL (−2.581 to 9.698 mL) versus −0.500 mL (−3.500 to 9.944 mL)], 30–60 mL [0.101 mL (−7.187 to 10.320 mL) versus 4.360 mL (−5.006 to 12.030 mL)], and >60 mL [−2.005 mL (−15.380 to 2.681 mL) versus 8.881 mL (−4.410 to 27.720 mL)] (Figure 6G-6L).
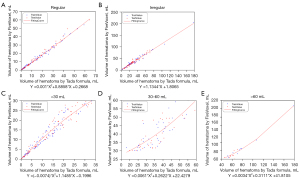
Table 3
| FireVoxel | N | Method | Bias (mL) | P2.5 (mL) | P97.5 (mL) | Limit of agreement (mL) |
|---|---|---|---|---|---|---|
| Groups divided by shape | ||||||
| Regular | 135 | Tada formula | −0.620 | −4.524 | 2.844 | −4.524 to 2.844 |
| C-Tada formula | −0.020 | −2.146 | 4.626 | −2.146 to 4.626 | ||
| Irregular | 110 | Tada formula | 4.170 | −2.844 | 19.470 | −2.844 to 19.470 |
| C-Tada formula | −0.530 | −9.321 | 10.820 | −9.321 to 10.820 | ||
| Groups divided by volume | ||||||
| <30 mL | 162 | Tada formula | −0.155 | −3.890 | 5.375 | −3.890 to 5.375 |
| C-Tada formula | −0.070 | −3.013 | 5.602 | −3.013 to 5.602 | ||
| 30–60 mL | 65 | Tada formula | 3.940 | −4.370 | 18.690 | −4.370 to 18.690 |
| C-Tada formula | −1.190 | −7.506 | 12.220 | −7.506 to 12.220 | ||
| >60 mL | 18 | Tada formula | 11.040 | −4.410 | 26.94 | −4.410 to 26.940 |
| C-Tada formula | −0.780 | −15.95 | 7.540 | −15.950 to 7.540 |
Table 4
| FireVoxel | N | Method | Bias (mL) | P2.5 (mL) | P97.5 (mL) | Limit of agreement (mL) |
|---|---|---|---|---|---|---|
| Groups divided by shape | ||||||
| Regular | 42 | Tada formula | −1.303 | −4.961 | 2.824 | −4.961 to 2.824 |
| C-Tada formula | 0.341 | −1.995 | 4.715 | −1.995 to 4.715 | ||
| Irregular | 42 | Tada formula | 7.393 | −1.669 | 26.540 | −1.669 to 26.540 |
| C-Tada formula | 1.290 | −10.960 | 5.819 | −10.960 to 5.819 | ||
| Groups divided by volume | ||||||
| <30 mL | 39 | Tada formula | −0.500 | −3.500 | 9.944 | −3.500 to 9.944 |
| C-Tada formula | −0.204 | −2.581 | 9.698 | −2.581 to 9.698 | ||
| 30–60 mL | 34 | Tada formula | 4.360 | −5.006 | 12.030 | −5.006 to 12.030 |
| C-Tada formula | 0.101 | −7.187 | 10.320 | −7.187 to 10.320 | ||
| >60 mL | 11 | Tada formula | 8.881 | −4.410 | 27.720 | −4.410 to 27.720 |
| C-Tada formula | −2.005 | −15.380 | 2.681 | −15.380 to 2.681 |
Additionally, the percentage deviation from FireVoxel for the Tada formula was greatly reduced for all hematoma shapes after correction with the C-Tada formula (all P<0.001) (Table 5, Figure 7A). Equally, applying the C-Tada formula to the groups divided by volume, the results showed that the percentage deviation in the 30–60 mL and >60 mL groups was significantly reduced (P<0.001) (Table 5, Figure 7B). However, there was very little decrease in the calculated volume for the <30 mL group (P=0.247) (Table 5, Figure 7B), illustrating that the C-Tada formula based on shapes may be more accurate than that based on volumes. Similarly, lower percentage deviation of C-Tada formulas was reconfirmed by the test dataset (Regular and Irregular all P<0.001; <30 mL: P=0.928, 30–60 mL: P=0.003, >60 mL: P<0.001) (Table 6, Figure 7C,7D).
Table 5
| Percentage deviation from FireVoxel, % | N | Method | Median | Maximum | Minimum | P75 | P25 | IQR | P value |
|---|---|---|---|---|---|---|---|---|---|
| Groups divided by shape | |||||||||
| Regular | 135 | Tada formula | 6.34 | 34.97 | −27.50 | 12.20 | −4.77 | 16.97 | <0.001 |
| C-Tada formula | 0.64 | 37.81 | −29.67 | 4.07 | −8.85 | 12.92 | |||
| Irregular | 110 | Tada formula | −16.43 | 20.85 | −43.58 | −8.97 | −23.04 | 14.04 | <0.001 |
| C-Tada formula | 1.41 | 51.82 | −30.45 | 9.97 | −6.02 | 15.99 | |||
| Groups divided by volume | |||||||||
| <30 mL | 162 | Tada formula | 2.83 | 34.97 | −43.20 | 11.85 | −14.28 | 26.13 | 0.247 |
| C-Tada formula | 0.50 | 42.88 | −39.38 | 14.31 | −14.30 | 28.61 | |||
| 30–60 mL | 65 | Tada formula | −11.47 | 12.02 | −43.58 | 2.00 | −21.77 | 23.77 | <0.001 |
| C-Tada formula | 3.18 | 24.31 | −28.31 | 9.44 | −7.55 | 16.99 | |||
| >60 mL | 18 | Tada formula | −13.99 | 7.35 | −28.69 | −11.28 | −19.33 | 8.05 | <0.001 |
| C-Tada formula | 0.76 | 26.57 | −9.09 | 6.39 | −2.86 | 9.25 |
IQR, interquartile range.
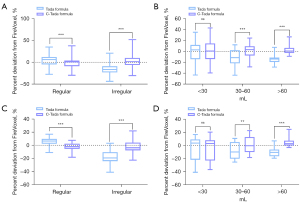
Table 6
| Percentage deviation from FireVoxel, % | N | Method | Median | Maximum | Minimum | P75 | P25 | IQR | P value |
|---|---|---|---|---|---|---|---|---|---|
| Groups divided by shape | |||||||||
| Regular | 42 | Tada formula | 6.46 | 16.87 | −11.01 | 9.76 | 2.36 | 7.40 | <0.001 |
| C-Tada formula | −1.97 | 7.61 | −18.03 | 2.44 | −5.28 | 7.72 | |||
| Irregular | 42 | Tada formula | −19.21 | 3.25 | −40.90 | −10.43 | −24.04 | 13.61 | <0.001 |
| C-Tada formula | −3.68 | 21.96 | −22.52 | 4.00 | −7.65 | 11.65 | |||
| Groups divided by volume | |||||||||
| <30 mL | 39 | Tada formula | 3.81 | 16.87 | −40.90 | 9.32 | −21.69 | 31.01 | 0.928 |
| C-Tada formula | 3.16 | 20.35 | −36.81 | 8.00 | −22.98 | 30.98 | |||
| 30–60 mL | 34 | Tada formula | −9.77 | 10.79 | −25.41 | 5.31 | −20.06 | 25.37 | 0.003 |
| C-Tada formula | −0.29 | 22.71 | −18.31 | 13.00 | −9.96 | 22.96 | |||
| >60 mL | 11 | Tada formula | −10.44 | 7.07 | −19.29 | −6.24 | −16.41 | 10.17 | <0.001 |
| C-Tada formula | 2.90 | 24.67 | −2.96 | 7.50 | −0.01 | 7.51 |
IQR, interquartile range.
Discussion
ICH is a critical and dangerous disease and has become the leading cause of death and disability worldwide (15-17). Related studies note that when the volume of ICH is small, conservative treatment should be selected. In contrast, larger hemorrhages should be treated with relatively active surgical treatment (2). The volume of bleeding can be used as a criterion for judging surgical indications; in general, the surgical indications for supratentorial ICH are hematoma volume >20 to 30 mL with GCS scores in the moderate range [5–12], midline structure shift >1.0 cm, bleeding into the ventricle, and significant pressure on the cistern. In addition, one of the most important reasons to calculate ICH volume, especially early, is prognostication. ICH volume is one of the points given for ICH score calculation. A very significant corner stone for intervention versus no intervention is an ICH score of 2 versus 3. An ICH score of 2 carries a mortality rate of 26%, while an ICH score of 3 carries a mortality rate of 72%. Other components of the ICH score are the Glasgow Coma Score (GCS), age ≥80 years, intraventricular hemorrhage and infratentorial origin of the hemorrhage (18). On many occasions, patients receive two points for a decline in GCS and age, and thus, ICH volume becomes a critical point in determining prognosis. There are many methods to measure the volume of intracranial hematoma, such as the Peterson formula, the Tada formula, software-based measurements, and the calculus method (10,19,20). At present, the most widely used clinical method for measuring intracranial hematoma is the Tada formula method, which was first proposed by Japanese scholars: V=1/2×A×B×C, where A (mm) is the maximum hematoma length, B (mm) is the maximum width perpendicular to A (mm) determined on the slice of maximal area, and C is the depth of hematoma. In theory, this formula idealizes the regular hematoma shape as an ellipsoid and ignores volume defects of irregular hematomas, which ultimately overestimates the actual volume (21-23). Clinically, some patients who should be conservatively treated may be included for surgical treatment, which could lead to unnecessarily increased trauma and complications and prolonged healing time. Therefore, the Tada formula measurement method cannot fully meet all clinical needs for calculating the hematoma volume. The results of this study are consistent with this conclusion.
The Tada 1/2ABC formula is applicable for patients whose hematoma shape is similar to round or ellipsoid, while the 1/3ABC formula is applicable for irregular shapes. However, the Tada formula always produces large errors of overestimation (1/2ABC) or underestimation (1/3ABC). In this study, the volume of the hematomas measured by FireVoxel was shown to be similar to the actual premeasured volumes. FireVoxel and the Tada formula (1/2ABC for regular and 1/3ABC for irregular) were used to calculate the volumes of hematomas of different shapes. The hematoma volume measured by the two methods was compared between groups divided by shape and volume, and there was a tendency for overmeasurement with greater hematoma volumes for regularly shaped hematomas with the 1/2ABC Tada and a tendency to underestimate irregularly shaped hematomas with the 1/2ABC Tada. The percentage deviation from the FireVoxel volume calculated by the Tada formula was different among the groups (both the shape and volume groups). The irregular group had higher percentage deviations than the regular group, while the 30–60 mL group and >60 mL group had higher percentage deviations than the <30 mL group. The reason may be that the surface area to volume ratio (S/V) of irregular intracranial hematomas is larger than that of regular hematomas. These data indicate that these shapes are far from an ellipsoid, leading to differences in the accuracy of the calculation results. Although the volume of the hematoma measured by FireVoxel was shown to be similar to that of the standard, use of this software is inconvenient for clinical application, given the image format requirements and insufficient time for manual delineation. To improve the accuracy of the Tada formula for measuring hematoma volumes, polynomial fitting was employed to determine the correlation between the volume measured by the Tada formula and FireVoxel. The percentage deviation from FireVoxel was greatly reduced for all hematoma shape and volume groups after correction by the polynomial fitting formulas (C-Tada formulas), and these deviations were all statistically significant except for the <30 mL group in the training test data, while all deviations showed great differences for each group in the test dataset. These results demonstrate that the C-Tada formulas based on shape may be more accurate and reliable than those based on volume.
The Tada formula, namely, π/6ABC, has been adapted into various new formulas, such as 1/2ABC, 1/3ABC, and 2/3SH. 1/2ABC is widely used, but it has a tendency to overestimate the hematoma volume, with a median percentage deviation of 6.69% (10), which is similar in our study, 6.34%. Through the corresponding C-Tada formula, the median percentage deviation was reduced to 0.64%. 1/3ABC is considered to be more suitable for irregular hematoma, with a median percentage deviation of −10.25% (10), which is −16.43% in our study. Using the corresponding C-Tada formula, the median percentage deviation was decreased to 1.41%. Although 2/3SH was reported to be more accurate than 1/2ABC, it has not been widely used in clinical practice and requires further study. The C-Tada formula was generated on the basis of Tada 1/2ABC and Tada 1/3ABC, reducing the overestimation of Tada 1/2ABC and underestimation of Tada 1/3ABC, which will make the Tada formula (1/2ABC for regular and 1/3ABC for irregular) more accurate. As stated earlier in the manuscript, first, the Tada formula (1/2ABC for regular and 1/3ABC for irregular) is used to calculate the volume of the hematoma, and then, the volume is corrected with the corresponding C-Tada formula, which improves the accuracy of the original formula while maintaining its high efficiency. Consequently, the C-Tada formula can be embedded in Microsoft Excel in the doctor’s station so that measurements can be performed anytime and anywhere, providing an accurate basis for the selection of clinical treatments for intracranial hemorrhage.
A few limitations of this study should be mentioned. Since undetailed shape classification leads to some missing information and volume estimation based on the inaccurate Tada formula, the C-Tada formula is only partially corrected for this inaccuracy and is imperfect, while it maintains the efficiency of volume calculation. When applying the C-Tada formula to the diagnosis and treatment of ICH, the slight overestimation of the actual volume should also be considered. Fortunately, the requirements for hematoma volume measurement in ICH treatment decisions are not very precise, which also makes the C-Tada formula clinically practical. Additionally, the accuracy of the C-Tada formula in ICH volume calculation needs to be validated with more clinical data.
Conclusions
It is important for clinicians to evaluate the volume of the hematoma to help determine further treatment. Although the Tada formula is widely used, this method is inaccurate. The C-Tada formula is a relatively accurate method, maintains the high efficiency of the Tada formula, and could have a positive role in the clinical measurement of hematomas with large volumes or irregular shapes.
Acknowledgments
Funding: This work was supported by the National Natural Science Foundation of China (Nos. 82071390, 82101434 and 61976241); Beijing Tianjin Hebei Basic Research Cooperation Project [No. 19JCZDJC64600(Z)]; and Tianjin Research Program of Application Foundation and Advanced Technology (No. 19YFZCSY00650).
Footnote
Reporting Checklist: The authors have completed the GRRAS reporting checklist. Available at https://qims.amegroups.com/article/view/10.21037/qims-22-1084/rc
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://qims.amegroups.com/article/view/10.21037/qims-22-1084/coif). The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). This study was approved by the Institutional Ethics Committee of Tianjin Medical University General Hospital, and all participants provided written informed consent.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Puy L, Parry-Jones AR, Sandset EC, Dowlatshahi D, Ziai W, Cordonnier C. Intracerebral haemorrhage. Nat Rev Dis Primers 2023;9:14. [Crossref] [PubMed]
- Mazzoleni V, Padovani A, Morotti A. Emergency management of intracerebral hemorrhage. J Crit Care 2023;74:154232. [Crossref] [PubMed]
- Morotti A, Boulouis G, Dowlatshahi D, Li Q, Shamy M, Salman RA, Rosand J, Cordonnier C, Goldstein JN, Charidimou A. Intracerebral haemorrhage expansion: definitions, predictors, and prevention. Lancet Neurol 2023;22:159-71. [Crossref] [PubMed]
- Toffali M, Carbone F, Fainardi E, Morotti A, Montecucco F, Liberale L, Padovani A. Secondary prevention after intracerebral haemorrhage. Eur J Clin Invest 2023; Epub ahead of print. [Crossref] [PubMed]
- Brown DL, Morgenstern LB. Stopping the bleeding in intracerebral hemorrhage. N Engl J Med 2005;352:828-30. [Crossref] [PubMed]
- Tuhrim S. Intracerebral hemorrhage--improving outcome by reducing volume? N Engl J Med 2008;358:2174-6. [Crossref] [PubMed]
- Broderick JP, Brott TG, Duldner JE, Tomsick T, Huster G. Volume of intracerebral hemorrhage. A powerful and easy-to-use predictor of 30-day mortality. Stroke 1993;24:987-93. [Crossref] [PubMed]
- Lindner A, Kunst S, Ianosi BA, Rass V, Schiefecker AJ, Kofler M, Limmert V, Grams AE, Pfausler B, Beer R, Thomé C, Helbok R. The location of intraparenchymal bleeding determines functional outcome after spontaneous subarachnoid hemorrhage. Eur J Neurol 2023;30:372-9. [Crossref] [PubMed]
- Ruiz-Sandoval JL, Chiquete E, Romero-Vargas S, Padilla-Martínez JJ, González-Cornejo S. Grading scale for prediction of outcome in primary intracerebral hemorrhages. Stroke 2007;38:1641-4. [Crossref] [PubMed]
- Huttner HB, Steiner T, Hartmann M, Köhrmann M, Juettler E, Mueller S, Wikner J, Meyding-Lamade U, Schramm P, Schwab S, Schellinger PD. Comparison of ABC/2 estimation technique to computer-assisted planimetric analysis in warfarin-related intracerebral parenchymal hemorrhage. Stroke 2006;37:404-8. [Crossref] [PubMed]
- Zhao B, Jia WB, Zhang LY, Wang TZ. 1/2SH: A Simple, Accurate, and Reliable Method of Calculating the Hematoma Volume of Spontaneous Intracerebral Hemorrhage. Stroke 2020;51:193-201. [Crossref] [PubMed]
- Sha Z, Song Y, Wu Y, Sha P, Ye C, Fan G, Gao S, Yu R. The value of texture analysis in peritumoral edema of differentiating diagnosis between glioblastoma and primary brain lymphoma. Br J Neurosurg 2020; Epub ahead of print. [Crossref] [PubMed]
- Barras CD, Tress BM, Christensen S, MacGregor L, Collins M, Desmond PM, Skolnick BE, Mayer SA, Broderick JP, Diringer MN, Steiner T, Davis SM. Density and shape as CT predictors of intracerebral hemorrhage growth. Stroke 2009;40:1325-31. [Crossref] [PubMed]
- Fujii Y, Tanaka R, Takeuchi S, Koike T, Minakawa T, Sasaki O. Hematoma enlargement in spontaneous intracerebral hemorrhage. J Neurosurg 1994;80:51-7. [Crossref] [PubMed]
- Liu M, Wu B, Wang WZ, Lee LM, Zhang SH, Kong LZ. Stroke in China: epidemiology, prevention, and management strategies. Lancet Neurol 2007;6:456-64. [Crossref] [PubMed]
- Feigin VL, Roth GA, Naghavi M, Parmar P, Krishnamurthi R, Chugh S, Mensah GA, Norrving B, Shiue I, Ng M, Estep K, Cercy K, Murray CJL, Forouzanfar MH. Global burden of stroke and risk factors in 188 countries, during 1990-2013: a systematic analysis for the Global Burden of Disease Study 2013. Lancet Neurol 2016;15:913-24. [Crossref] [PubMed]
- Lu P, Cao Z, Gu H, Li Z, Wang Y, Cui L, Wang Y, Zhao X. Association of sex and age with in-hospital mortality and complications of patients with intracerebral hemorrhage: A study from the Chinese Stroke Center Alliance. Brain Behav 2023;13:e2846. [Crossref] [PubMed]
- Hemphill JC 3rd, Bonovich DC, Besmertis L, Manley GT, Johnston SC. The ICH score: a simple, reliable grading scale for intracerebral hemorrhage. Stroke 2001;32:891-7. [Crossref] [PubMed]
- Chung KJ, Kuang H, Federico A, Choi HS, Kasickova L, Al Sultan AS, Horn M, Crowther M, Connolly SJ, Yue P, Curnutte JT, Demchuk AM, Menon BK, Qiu W. Semi-automatic measurement of intracranial hemorrhage growth on non-contrast CT. Int J Stroke 2021;16:192-9. [Crossref] [PubMed]
- Freeman WD, Barrett KM, Bestic JM, Meschia JF, Broderick DF, Brott TG. Computer-assisted volumetric analysis compared with ABC/2 method for assessing warfarin-related intracranial hemorrhage volumes. Neurocrit Care 2008;9:307-12. [Crossref] [PubMed]
- Webb AJ, Ullman NL, Morgan TC, Muschelli J, Kornbluth J, Awad IA, et al. Accuracy of the ABC/2 Score for Intracerebral Hemorrhage: Systematic Review and Analysis of MISTIE, CLEAR-IVH, and CLEAR III. Stroke 2015;46:2470-6. [Crossref] [PubMed]
- Xu X, Chen X, Zhang J, Zheng Y, Sun G, Yu X, Xu B. Comparison of the Tada formula with software slicer: precise and low-cost method for volume assessment of intracerebral hematoma. Stroke 2014;45:3433-5. [Crossref] [PubMed]
- Wang CW, Juan CJ, Liu YJ, Hsu HH, Liu HS, Chen CY, Hsueh CJ, Lo CP, Kao HW, Huang GS. Volume-dependent overestimation of spontaneous intracerebral hematoma volume by the ABC/2 formula. Acta Radiol 2009;50:306-11. [Crossref] [PubMed]


