Hierarchical K-means clustering method for accelerated Lorentzian estimation (KALE) in chemical exchange saturation transfer-magnetic resonance imaging quantification

Introduction

Chemical exchange saturation transfer imaging (CEST) magnetic resonance imaging (MRI) can be used to indirectly image low concentration components with enhanced sensitivity by measuring the deprivation of water signals caused by the exchange of selectively saturated protons. The specific radiofrequency (RF) labeling of solute protons in CEST allows for the imaging of targeted metabolites (1-5). Due to the pH sensitivity of the chemical exchange process (6-8), CEST can also measure changes in the microenvironment, i.e., changes in pH. Therefore, CEST MRI has great potential in clinical applications such as the detection of ischemic stroke, tumors, and neurologic diseases.

CEST images are acquired as a function of saturation frequency offsets, generating the so-called Z-spectrum. However, multiple signal components are shown as overlapping effects in the Z-spectrum, including direct water saturation (DS) (9), the magnetic transfer (MT) effect (9-11) from macromolecules, the nuclear Overhauser effects (NOEs) from mobile macromolecules (12-14), and the CEST effects from multiple types of exchangeable protons such as creatine (4,15,16), phosphocreatine (17-19), glycogen (20-22), amide (23-25), and amine (15,26,27). Line shape fitting-based quantification methods have been proposed to quantify these effects by fitting the experimental data with multipool models [multipool Lorentzian fitting (LF)] (26,28,29) or by taking the difference of raw Z-spectra and the fitted background spectra [Lorentzian difference (LD) analysis] (30-32). The LD and multipool Lorentzian allow the estimation of peak amplitude, peak width and centered offset for multiple proton pools and therefore have been increasingly used in a wide range of preclinical and clinical studies (33,34). However, generating contrast maps by voxelwise fitting results in high computational costs, which increase dramatically with image size and fitting complexity. In addition, the fitting results are easily affected by image noise, Z-spectrum oscillations and the initial values of iterative optimization. These obstacles have greatly hindered CEST applications, especially for clinical situations with a weak CEST signal of a few percent and a large dataset with multiple slices.

To tackle the obstacles, an “image downsampling expedited adaptive least-squares (IDEAL)” approach (35) was developed, which creatively used voxel-grouping by multilevel downsampling and fitting updates to generate contrast maps. Despite its improved denoising performance, IDEAL used a fixed-square subgroup downsampling strategy, resulting in intensity dilution and loss of detailed structure information in the contrast map. Later, another study used a similar voxel grouping idea to IDEAL but further integrated K-means for voxel clustering (36). Since K-means can intelligently group voxels according to the image structure, this study significantly improved B₀ correction using 1-pool LF. However, this study did not calculate contrast maps from LF.

In this study, we develop a K-means clustering method for accelerated Lorentzian estimation (KALE) approach to calculate CEST contrast maps based on LF of Z-spectra. KALE groups voxels using K-means clustering according to their Z-spectral similarities, and only a single fitting is required within each group. Subgrouping and ‘groupwise’ fitting are performed hierarchically at multiple levels, with the initial values and boundaries updated adaptively for each group. We first optimize and validate KALE implemented with LD quantification using multislice healthy human brain data acquired at 2 T. Then, for the ischemic rat brain acquired at 7 T, KALE is further evaluated for implementation with LD and with five-pool LF.

Methods

Hierarchical K-means clustering and transitional fitting parameters

K-means clustering is a simple and popular clustering method. Under the K-means++ strategy (37), K-means clustering classifies voxels into a designated number (K) of groups based on the distance of each voxel from K centroids (37). In CEST MRI, the Z-spectra differ greatly among varying tissues and abnormal regions but resemble each other within similar tissues or microenvironments. By clustering voxels with similar Z-spectra, the computational cost of LF can be greatly reduced. Thus, we proposed a KALE method that conducts K-means clustering iteratively in a top-down manner and optimizes the fitting parameters (and boundaries) of LF in a groupwise manner.

Figure 1 illustrates the KALE method. K-means clustering separates the Z-spectra of all image voxels into different groups by the K-means++ strategy. A group is regarded as fine-clustered (labeled in green) if it satisfies one of the two termination criteria (described below). Otherwise, the group is further clustered until each subcluster is fine-clustered. The whole process is implemented using the breadth-first search (BFS) strategy (38), and a demonstration of hierarchical clustering is shown in Figure S1.

Figure 1 An illustrative flowchart of the proposed method. The whole S₀-normalized CEST image series is input to the K-means++ clustering method. K=2 is used for illustration. Output1 and output2 correspond to KALE with the Lorentzian difference and the parameter set, as described in A. KALE with the multipool Lorentzian fitting update parameters in the strategy described in B has the final parameters as output. The details can be found in the Methods section, “Hierarchical k-means clustering and transitional fitting parameters”. LF, Lorentzian fitting; CEST, chemical exchange saturation transfer; KALE, K-means clustering method for accelerated Lorentzian estimation.

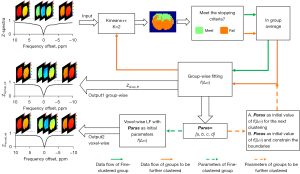
To minimize tissue variation within the group, the criteria for the termination of clustering are set according to the standard deviation of voxel values or the number of voxels:

σ/cluster<σbrainRs[1]

N/cluster<N/imageRN2[2]

where σ_cluster and σ_brain are the standard deviations (σ) of the measured Z-spectral intensities for voxels within a cluster and for voxels within the entire brain, respectively; N_/cluster and N_/image are the voxel number within a cluster and the voxel number in the image, respectively; and R_S and RN2 are the trade-off parameters determined by the ratio of σ_brain and σ_cluster and N_/image and N_/cluster, respectively. Eq. [1] constrains the signal intensities within a group to a small standard deviation, and Eq. [2] restricts the voxel numbers within a group according to the full image size. Since the restriction is on a two-dimensional image, R_N is set as the squared term. The choice of clustering number K and clustering termination criteria R_s and R_N are discussed in the Results Section “KALE with LD”.

K-means integrated with the LD

The single-pool LF (39) process is first embedded in the clustering iteration.

f(Δω)=d+b1+4×(Δω−ac)2[3]

where Δω is the frequency offset from water resonance and a, b, and c are the frequency offset, amplitude, and linewidth of water, respectively. d is the baseline constant.

The LF of the group-averaged Z-spectra is conducted for each group, generating a fitted reference Z-spectra (Z_group,fit) and a set of parameters (Paras = [a, b, c, d]). The iterative step is only executed for groups that need to be further clustered. Paras of these groups are used as initial values for fitting of the group-average Z-spectra in the next loop of finer clustering. Finally, the groupwise fitted Z-spectra (Z_group,fit) of all fine-clustered groups are merged as the groupwise reference signal Z_{kgroup_ref}. Moreover, the groupwise optimized parameters Paras are used as initial values for voxelwise LF to generate Z_{kvoxel_ref}. Therefore, the LD images can be obtained by two strategies, including (I) subtracting the experimental Z-spectra from the voxelwise fitting (Z_{kvoxel_ref}), marked as LD_voxel-k; and (II) taking the difference of the groupwise reference spectra (Z_{kgroup_ref}) and the group-averaged Z-spectra, marked as LD_group-k.

K-means integrated with multipool LF

Then, the KALE concept is combined with multipool LF, including water, amide, amine, NOE, and MT pools:

1−MzM0=∑i=1Nbi1+4×(Δω−aici)2[4]

where M_z and M₀ are the Z-spectra with and without saturation and a_i, b_i and c_i are the frequency offset, amplitude and line width of the peak for the i^th pool, respectively.

The basic scheme is similar to KALE with LD. However, in KALE with multipool fitting, only Paras are recorded. For non-fine-clustered groups, Paras are used as initial values and to constrain the boundaries of fitting parameters (Eq. [5-7]) for further fitting the group-averaged Z-spectra over loops. For fine-clustered groups, each voxel within the group is fitted with Paras as the initial fitting parameters, with boundaries set as follows:

[alow,ahigh]=[a−12λ,a+12λ][5]

[blow,bhigh]=[b−10∗λ,b+10∗λ][6]

[clow,chigh]=[c−100∗λ,c+100∗λ][7]

where [a_low, a_high], [b_low, b_high], and [c_low, c_high] are the boundaries of the frequency offset (ppm), amplitude and line width (ppm) of a pool, respectively. For group m, λ is set as the largest standard deviation of the Z-spectral data among the different frequency offsets:

λ=maxϖ(σ(ZΔϖ(clusterm)))[8]

where Z_Δω is the Z-spectral intensity (M_z/M₀) at Δω.

The order of the standard deviation for a cluster is usually 10⁻²; thus, 10*λ and 100*λ are of the same order of amplitude and linewidth, respectively. Since we assumed that the voxels within a cluster have a similar structure with a relatively homogeneous B₀ field, the fitting boundary for the offset is set as the range e of the standard deviation, which is ±(1/2)*λ.

Animal experiments

Experiments were performed under a project license granted by the ethics committee of Weifang Medical University in compliance with the institutional guidelines of Weifang Medical University for the care and use of animals. The animals used in the experiments were adult male Sprague-Dawley rats weighing 240 to 250 g. The stroke model used in this research was transient focal cerebral ischemia, where the rat experienced a 2-hour middle cerebral artery occlusion (MCAO) via intraluminal suture following reperfusion performed two hours post MCAO by withdrawing the nylon suture. During surgery, the body temperature of the rat was maintained at 37–37.5 ℃.

Brain MR imaging was performed at 2 hours post transient MCAO surgery on a Biospec 7 Tesla horizontal scanner (Bruker, Germany) with a transmit-receiver volume coil (diameter =40 mm). The rats were anesthetized by first applying ~4% isoflurane and then maintained at 1–2% during data acquisition. Multislice T_2W images were first acquired. Then, a 1 mm thick coronal slice at the center of the striatum was selected for the collection of both water saturation shift referencing (WASSR) (40) and CEST images. The imaging sequence consists of a continuous-wave presaturation pulse (T_sat =2,500 ms) and a rapid acquisition with relaxation enhancement (RARE) readout [RARE factor =32, repetition time/echo time (TR/TE) =5,000 ms/4 ms]. With B_1sat = 0.7 µT, a total of 51 Z-spectra images were collected from −10 to 10 ppm. WASSR images were collected by a weak saturation pulse (B_1sat =0.5 µT, T_sat =500 ms) with Δω incremented from −1 to 1 ppm (0.1 ppm step size) to correct B₀ inhomogeneity. The M₀ image without saturation at 66 ppm was acquired for data normalization. Other imaging parameters were field of view (FOV) =34×28 mm² and matrix size =64×64.

Healthy volunteers

Five healthy volunteers were recruited for brain data acquisition to validate KALE on clinical data. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). The study was approved by the institutional review board, Tsinghua University, China, and informed consent was obtained from all the subjects. MR data were collected on a 3.0 Tesla Philips scanner (Ingenia, Philips Health Care, Amsterdam, The Netherlands) with a 32-channel phase array.

CEST images were acquired using a 3D APT sequence with turbo spin echo readout on a 7 mm thick axial slice selected from T_2W images. A 40×50 ms Gaussian-shaped saturation pulse with a 100% duty cycle was used. Other imaging parameters of CEST images were as follows: T_sat =2 s, B_1sat =0.7 µT, 31 frequency offsets (i.e., ±0.5, 0.8, ±1, 1.2, 1.7, 1.9, ±2.1, 2.3, 2.5, ±3, +3.4, ±3.5, +3.6, +3.7, ±4, +4.5, ±5, ±6, ±8, ±10 ppm), TR =5 s, TE =7.8 ms, FOV =220×186 mm² with an acquisition voxel size of 2×2×7 mm³, and 5 slices. For better visualization, the vendor provided finer reconstruction images of 256×256 using zero-padding, which was used by all the following CEST analyses. The M₀ image at −1,560 ppm was acquired for data normalization. WASSR images (40) were collected for B₀ correction, with the same saturation time and power as animal scanning. Multislice T_2W images were acquired with a slice thickness of 1.5 mm, TR =5,000 ms, and TE =336 ms. T₁w images were collected with a slice thickness of 1.25 mm and TR/TE of 6.5/3.2 ms.

Data analysis

All data were processed by custom written MATLAB code on a computer with an Intel(R) Core(TM) i7-9700K processor, a 3.60 GHz CPU, and 32 G RAM. The saturation data were first corrected for B₀ inhomogeneity by the WASSR map and then interpolated by the MATLAB function “spline” with a step size of 0.1 ppm. The B₀ corrected image series were then normalized by the M₀ image. The computation time was accessed by MATLAB function “tic” “toc” from the start to the end of the fitting process (excluding data preprocessing).

Determination of trade-off parameters RS and RN

To determine the proper R_S and R_N values, the structural similarity index (SSIM) (41) and peak signal-to-noise ratio (PSNR) (36) were calculated between the groupwise Lorentzian estimation of the whole image and the raw input saturated data at −10 to −6.25 ppm, −2 to 2 ppm and 6.25 to 10 ppm:

SSIM(x,y)=(2μxμy+c1)(2σxy+c2)(μx2+μy2+c1)(σx2+σy2+c2)[9]

where x is the fitted data and y is the raw normalized CEST data (M_z/M₀); μ_x and μ_y are the mean values for x and y, respectively; σ_x and σ_y are the standard deviations of x and y, respectively; σ_xy is the covariance between x and y; and c₁=(k₁L)² and c₂=(k₂L)² are two constants to stabilize the division with a weak denominator, in which L is the dynamic range of the voxel values and by default k₁=0.01 and k₂=0.03.

PSNR(x,y)=10log10(peakvalue2MSE(x,y))[10]

where peakvalue is set to 1, and MSE is the mean square error of x and y.

LF details

For the single-pool fitting, the initial parameters for both KALE and traditional LF were set arbitrarily. Z-spectra within (−10 to −6.25), (−2 to 2) and (6.25 to 10) ppm were used in fitting.

For 5-pool fitting, the whole Z-spectra were fed into the fitting. The initial value and boundaries of the fitting parameters for both KALE and the traditional method were set as shown in Table 1 (42).

For both the traditional methods and KALE, the MATLAB-embedded function ‘lsqcurvefit’, a nonlinear least-squares solver, was used with the ‘lenvenberg-marquardt’ algorithm for optimization. The termination tolerance on the function value was set to 1e-10, and the maximum number of function evaluations was set to 10,000. The optimization was solved numerically by the finite difference method without using the Jacobian matrix.

Evaluation of the fitting performance

The fitting performance of the traditional method and KALE was evaluated by calculating the coefficient of variation (COV) of the designated ROI, namely, the putamen for human data and the striatum of the normal hemisphere for rat data:

COV=σ(ROI)μ(ROI)[11]

where σ(ROI) and µ(ROI) are the standard deviation and the mean value of the ROI intensity, respectively.

The fitting goodness was calculated by the coefficient of determination (R²) (43),

R2=∑i=1N(yi^−y¯)2∑i=1N(yi−y¯)2[12]

where y_i is the Z-spectrum, y¯ is the mean of the Z-spectrum, yi^ is the fitted spectrum, and N is the number of voxels in the brain.

Robustness to noise

Six levels (σ=0.005, 0.01, 0.015, 0.02, 0.025, 0.03) of Gaussian noise were added to the human brain data with a clinical size to assess the robustness of KALE with LD to noise.

The significance in all statistics was analyzed by the Prism embedded paired t-test method. Groups were considered to be different when the P value was 0.05 or less between groups.

Results

KALE with LD

Determination of the K value and trade-off parameters

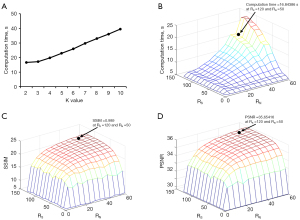
To determine the K value for K-means clustering and the proper termination criteria of clustering for data with a clinical size (256×256), we tested KALE on healthy human brain data. We first evaluated the choice of K value based on the total computation time, with the empirical R_N =50 and R_S =120. As shown in Figure 2A, the computation time increased dramatically when K was larger than 3; hence, it was set to 3. With K=3, R_N and R_S were determined by considering both the computation time and the fitting performance, including SSIM and PSNR. Since the clustering process could not converge for R_N beyond 60 and R_S beyond 130, R_N and R_S were tested from 0 to 60 and 130, respectively. As illustrated in Figure 2B-2D, the computation time group rose significantly when R_N was over 40 and R_S was over 50, while SSIM and PSNR increased slowly when R_N was over 40 and R_S was over 50. To achieve the best fitting performance within a sufficiently short computation time, R_S=120 and R_N =50 were chosen, where SSIM =0.989, PSNR =35.65, and the calculation time was 16.84 seconds per slice.

Figure 2 Optimization of the clustering parameters. (A) The relationship of the K value with the computation time; (B) the relationship of R_S and R_N with the computation time; (C) the relationship of R_S and R_N with the SSIM; (D) the relationship R_S and R_N with the PSNR. SSIM, structural similarity index measure; PSNR, peak signal-to-noise ratio; R_S and R_N, trade-off parameters.

The parameters for rat data were estimated by assuming a linear relationship between the clinical image size (256×256) and preclinical image size (64×64). Specifically, RN_preclinical=size_preclinical_image×size_clinical_imageRN_clinical2, and Rs_preclinical=σ(clinical_image)RS_clinical×σ(preclinical_image). Thus, the coarsely estimated [R_S, R_N] for the periclinal data was [76, 13].

Evaluation on human data

As shown in Figure 3, for Z-spectra without noise, the LD contrast maps of KALE were similar to the traditional results. Whereas the CEST image series interfered with by Gaussian noise of σ=0.01, the LD_group-k method performed better than the others, with similar contrast to the clear one. To evaluate the performance of the methods influenced by noise, the COVs within the putamen (ROIs plotted in Figure 3B) were calculated. Figure 3F,3G shows that the COV of the LD_group-k method was not affected by noise, while the COV of LD_voxel-k and the traditional method increased as the noise level increased. Additionally, the fitting results of five subjects (five slices per subject) were included for a statistical analysis of the computation time. The average computation times of the LD_group-k and LD_voxel-k methods per subject (five slices) were 2.18 and 4.82 min, respectively, which were significantly shorter than that of the traditional method (9.48 min) (Figure 3H, P<0.001).

Figure 3 Evaluation of KALE on human data with different noise levels. (A) B₀ map; (B) T_1W map, the red line highlights the ROIs analyzed in (F,G); (C) T_2W map; (D,E) amide (3.5 ppm) and NOE (−3.5 ppm) maps of the traditional method and our method (LD_voxel-k, voxelwise LD result; LD_group-k, groupwise LD result). (F,G) COV of amide (3.5 ppm) and NOE (−3.5 ppm) in the ROIs for three methods, where the traditional method is denoted in red lines, LD_group-k in blue and LD_voxel-k in green. (H) The statistical result of the computing time for the five subjects. P value by the paired t-test in Prism (***, P<0.001). LD, Lorentzian difference; NOE, nuclear Overhauser effects; COV, coefficient of variation; KALE, K-means clustering method for accelerated Lorentzian estimation; ROI, region of interest.

Evaluation of stroke rat brain data

Then, the KALE framework with the LD on stroke rat brain data was evaluated, as shown in Figure 4. The KALE summarized voxelwise LF (4,096 voxels in a CEST image) into 107 groupwise LF for a Z-spectral image series. Voxelwise KALE fitted the data with the groupwise optimized fitting parameters, achieving the same result as the traditional LD, with the computation time reduced from 7 to 2 s. Statistically, the computation time for six rats showed a significant decrease for both groupwise and voxelwise KALE (Figure 4D). Since only the initial parameters were optimized, the contrast and spectrum of voxelwise KALE closely resembled the traditional method on both the image (Figure 4C) and the spectra (Figure S2A,S2B).

Figure 4 LD analysis of ischemic stroke rat data. (A) The T_2W image with an ROI on the lesion side (ROI1, red circle) and a contralateral ROI (ROI2, blue circle). (B) B₀ map obtained by WASSR. (C) Top: the contrast map at 3.5 ppm by traditional LD analysis, voxelwise KALE (LD_voxel-k) and groupwise KALE (LD_group-k). Bottom: the contrast map at −3.5 ppm, same layout as the top row. (D) The statistical result of computing time for six rats. P value by the paired t-test in Prism (***, P<0.001). (E) ROI plotted to analyze the performance of groupwise KALE. (F) The averaged value by groupwise KALE with the final cluster number of the ROI on the APT and NOE contrast maps. LD, Lorentzian difference; NOE, nuclear Overhauser effects; ROI, region of interest; APT, amide proton transfer; WASSR, water saturation shift referencing; KALE, K-means clustering method for accelerated Lorentzian estimation.

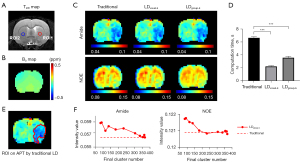
For the groupwise KALE, the image resolution was reduced due to the in-cluster averaging, which could be improved by increasing the final cluster number. An experiment on the final cluster number and the image intensity of groupwise KALE on rat data was performed, as shown in Figure 4F. The final cluster number was increased by adjusting the K value. The KALE-quantified values in the ischemic rat brain became stable and converged to the voxelwise LD, and the contrast maps were close to the traditional LD, as shown in Figure 4C, when the final cluster number was >330 at K=35. Although the increase in the K value costs more computation time, it is acceptable and still on the time scale of seconds given the small matrix size of the rat brain.

KALE with 5-pool LF

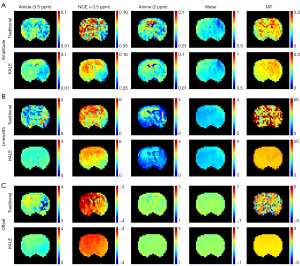
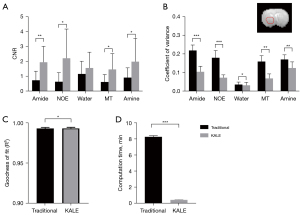
KALE was further integrated with 5-pool LF and tested on stroke rats with the same K value and clustering termination criteria as the KALE_LD animal experiments. As shown in Figure 5 and Figure 6A, KALE improved the image quality of the amplitude maps, and the contrast-to-noise ratio (CNR) (44) between lesion and contralateral tissue was significantly improved for all six rats on two sets of ROIs, as shown in Figure S3. Additionally, the fitted offset and linewidth maps were more homogeneous and less noisy in KALE (Figure 6B,6C), especially for the MT pool. The goodness of fit was then assessed by the COV of the ROI plotted on the normal hemisphere and R² (43) of the whole brain for both methods among the 6 rats. KALE had a smaller COV and higher R² than the traditional method for the five pools (Figure 6B,6C). The R² contrast maps of the two methods are shown in Figure S4, where two ROIs were drawn on the region with a higher value on the contrast map of KALE. Since the difference in the fitted spectra by the two methods (Figure S4) showed a larger variance for offsets within 1 to 5 ppm, the magnified spectra from 1 to 5 ppm are plotted in Figure S4, where KALE fitted the original data around 2 ppm better than the traditional method in ROI1, as indicated by the arrow. In addition to the improved fitting performance, the average computation time of 6 rats in KALE was 0.41 minutes (24.6 s), drastically decreased from that of 8.27 minutes by the traditional method (Figure 6C).

Figure 5 The parameter maps of KALE with 5-pool Lorentzian fitting and the traditional one. Each column from left to right, the amide pool (3.5 ppm), NOE pool (−3.5 ppm), amine pool (2 ppm), water pool and MT pool. (A) The amplitude contrast maps of traditional 5-pool Lorentzian fitting (first row) and KALE (second row). (B) Linewidth maps of traditional 5-pool Lorentzian fitting (first row) and KALE (second row). (C) The offset maps of traditional 5-pool Lorentzian fitting (first row) and KALE (second row). KALE, K-means clustering method for accelerated Lorentzian estimation; NOE, nuclear Overhauser effects; MT, magnetic transfer.

Figure 6 Statistical comparison of traditional 5-pool Lorentzian fitting (black bars) and KALE (gray bars) on data from 6 ischemic rats. (A) The CNR of the two methods for each pool was evaluated on the amplitude map using two sets of ROIs for each rat (as displayed in Figure S3, n=12). (B) The COV of the two methods for each pool was evaluated on the amplitude map for the ROI plotted on the normal hemisphere in red (n=6). (C) The brain average R² of the two methods on data from the six rats (n=6). The average R² is 0.993506 for KALE and 0.993438 for the traditional method. (D) The computation time of the two methods on the data from the six rats (n=6). The average computation time is 8.27 minutes for the traditional method and 24.6 seconds for KALE. P value by paired t-test in Prism (*, P<0.05; **, P<0.01; ***, P<0.001). CNR, contrast-to-noise ratio; NOE, nuclear Overhauser effects; MT, magnetic transfer; KALE, K-means clustering method for accelerated Lorentzian estimation; COV, coefficient of variation; ROI, region of interest; R², goodness of fit.

Discussion

CEST quantification approaches based on LF are increasingly employed in the research community, but traditional voxelwise fitting is sensitive to noise and initial parameters, with the computation time increasing dramatically with the number of voxels and fitting parameters. The developed KALE framework provides a fast and accurate method for CEST quantification maps by employing data-driven voxel grouping and parameter updating hierarchically. At each hierarchical level, voxels within a group are intelligently subgrouped by K-means clustering according to their Z-spectra similarity; then, only one fitting process is conducted in a subgroup using the groupwise optimized parameters. Tests on both the ischemic rat brain and healthy human brain demonstrated comparable or even superior CEST contrast maps with significantly reduced computation time compared to traditional voxelwise fitting. Smart and hierarchical data-driven voxel clustering and parameter updates may facilitate more preclinical and clinical CEST applications.

Since traditional voxelwise fitting methods fit the spectrum of each voxel separately, the computation time increases with the image size. Furthermore, the fitting process uses the same fixed parameters for all voxels, without taking into account the correlation and diversity among voxels. Therefore, for some voxels, many iteration steps are required to reach the optimized targets. Since KALE updates the parameters multiple times with varied initial values, the fitting process undergoes fewer iterations. For the rat data, the average number of iterations is 14–41 for the traditional LD and 5–10 for KALE. Apart from the computation time of the fitting process, KALE also requires time for clustering. However, the average clustering time is almost negligible compared to the time required for the fitting process and is only ~17 s for 1,961 final clusters of a human brain slice. Therefore, KALE can dramatically reduce the computation time by reducing both the number of fits and the number of iterations for each fit.

For each clustering level, KALE fits an averaged experimental spectrum of all voxels within the cluster, leading to improved noise reduction performance over traditional voxelwise LD (Figure 3D,3E). This study illustrates the denoising performance by adding simple Gaussian noise directly to the reconstructed magnitude images of the CEST series. However, real MR images contain noise from multiple sources and have complicated distributions, especially for multichannel readouts. More dedicated evaluations may be necessary in the future, e.g., utilizing Rician noise and Rician-bias correction.

Compared with the previous IDEAL approach, which performed fitting by the fixed ratio of squarish downsampling, KALE uses the same idea of voxel grouping to maintain the denoising performance. However, superior to IDEAL, KALE is more intelligent by clustering the voxels according to their Z-spectral similarity. Therefore, KALE achieves more accurate quantification maps with small structural details by avoiding contrast dilution from the voxel average (Appendix 1, Figures S5,S6). Note that the quantification accuracy and image detail of groupwise KALE is affected by the final cluster number, which is mainly determined by the K value and by the cluster termination criteria. Herein, different K values were investigated to determine the optimal final cluster number, as adjusting the termination criteria may cause clustering failure. The rat dataset suggested that K=35 could provide groupwise KALE with comparable results to the traditional method.

When implemented with multipool LF, KALE achieved quantification maps with higher CNR and better fitting goodness than the traditional voxel-by-voxel fitting approach, using only 1/20 of the computational time (0.41 vs. 8.27 minutes). This further illustrated KALE’s advantage in complicated multiparameter fitting, where 15 parameters were required for a 5-pool model, by updating both the initial values of the fitting parameters and their boundaries at each level of K-means clustering. The boundary constraints mainly included the standard deviation of voxels within each cluster among all offsets in the original Z-spectra (Eq. [4]). Thus, the possible abnormality of voxelwise fitting can be constrained by the groupwise information of neighboring voxels. KALE produced more homogeneous contrast maps compared to the results of the traditional method, as shown in Figure 5, with significantly reduced computation time.

In addition, the results on the ischemic rat data by KALE clearly showed half hemispheric hypointensity on the amide amplitude map (Figure 5), which was consistent with the results of previous studies (26,45,46). The lesion area on the amine contrast map showed a lower signal in a smaller area than on the amide map and is in agreement with the findings of Wu et al. (45) and Cui et al. (26). However, the opposite hyperintensity of the lesion was reported on the amine map (26,46). As discussed in Cui et al. (26), several effects at neighboring offsets also contributed to the signal at 2 ppm, which cannot be fully modeled by a single pool. Although the overall fitting performance was improved, with a lower COV in the normal region and higher R² (Figure 6), the extraction of signals was limited by the fitting model.

Currently, several machine learning-based methods have been proposed for CEST quantification (47-49). Although the online steps of machine learning-based methods are fast, the resulting contrast images are highly dependent on the training set or offline dictionary. Model-based fitting is currently the most widely used method for in vivo experiments. The basic idea of KALE, to update the fitting parameters in a groupwise manner based on the similarity within the same tissues or structures, could be implemented on other quantification methods such as polynomial and Lorentzian fitting (PLOF) (26,50), LAREX omega-plot analysis (51), and Bloch-McConnell fitting. Although KALE was only evaluated on brain images in this work, its robustness to outlier pixels such as vessels was demonstrated, as shown in Figure S6, suggesting the promising potential application of KALE on other structures. Notably, although motion correction was not required in this study, for application to other structures that are more prone to motion artifacts, motion correction methods (52) could be applied prior to the KALE approach to ensure performance.

Acknowledgments

Funding: This work was supported by the National Natural Science Foundation of China (NSFC) (Nos. 82071914 and 82071888).

Footnote

Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://qims.amegroups.com/article/view/10.21037/qims-22-1379/coif). The authors have no conflicts of interest to declare.

Ethical Statement: The authors are accountable for all aspects of the work and for ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). The study was approved by the institutional review board, Tsinghua University, China, and informed consent was obtained from all patients. Animal experiments were performed under a project license granted by the ethics committee of Weifang Medical University in compliance with the institutional guidelines of Weifang Medical University for the care and use of animals.

Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.

References

1. Jin T, Mehrens H, Wang P, Kim SG. Chemical exchange-sensitive spin-lock MRI of glucose analog 3-O-methyl-d-glucose in normal and ischemic brain. J Cereb Blood Flow Metab 2018;38:869-80. [Crossref] [PubMed]
2. Bagga P, Pickup S, Crescenzi R, Martinez D, Borthakur A, D'Aquilla K, Singh A, Verma G, Detre JA, Greenberg J, Hariharan H, Reddy R. In vivo GluCEST MRI: Reproducibility, background contribution and source of glutamate changes in the MPTP model of Parkinson's disease. Sci Rep 2018;8:2883. [Crossref] [PubMed]
3. Cui J, Zu Z. Towards the molecular origin of glutamate CEST (GluCEST) imaging in rat brain. Magn Reson Med 2020;83:1405-17. [Crossref] [PubMed]
4. Cai K, Tain RW, Zhou XJ, Damen FC, Scotti AM, Hariharan H, Poptani H, Reddy R. Creatine CEST MRI for Differentiating Gliomas with Different Degrees of Aggressiveness. Mol Imaging Biol 2017;19:225-32. [Crossref] [PubMed]
5. AlGhuraibawi W, Stromp T, Holtkamp R, Lam B, Rehwald W, Leung SW, Vandsburger M. CEST MRI reveals a correlation between visceral fat mass and reduced myocardial creatine in obese individuals despite preserved ventricular structure and function. NMR Biomed 2019;32:e4104. [Crossref] [PubMed]
6. Anemone A, Consolino L, Conti L, Irrera P, Hsu MY, Villano D, Dastrù W, Porporato PE, Cavallo F, Longo DL. Tumour acidosis evaluated in vivo by MRI-CEST pH imaging reveals breast cancer metastatic potential. Br J Cancer 2021;124:207-16. [Crossref] [PubMed]
7. Sun PZ, Zhou J, Sun W, Huang J, van Zijl PC. Detection of the ischemic penumbra using pH-weighted MRI. J Cereb Blood Flow Metab 2007;27:1129-36. [Crossref] [PubMed]
8. Pavuluri K, Manoli I, Pass A, Li Y, Vernon HJ, Venditti CP, McMahon MT. Noninvasive monitoring of chronic kidney disease using pH and perfusion imaging. Sci Adv 2019;5:eaaw8357. [Crossref] [PubMed]
9. van Zijl PCM, Lam WW, Xu J, Knutsson L, Stanisz GJ. Magnetization Transfer Contrast and Chemical Exchange Saturation Transfer MRI. Features and analysis of the field-dependent saturation spectrum. Neuroimage 2018;168:222-41. [Crossref] [PubMed]
10. Swanson SD, Malyarenko DI, Fabiilli ML, Welsh RC, Nielsen JF, Srinivasan A. Molecular, dynamic, and structural origin of inhomogeneous magnetization transfer in lipid membranes. Magn Reson Med 2017;77:1318-28. [Crossref] [PubMed]
11. Morrison C, Stanisz G, Henkelman RM. Modeling magnetization transfer for biological-like systems using a semi-solid pool with a super-Lorentzian lineshape and dipolar reservoir. J Magn Reson B 1995;108:103-13. [Crossref] [PubMed]
12. Zhang XY, Wang F, Li H, Xu J, Gochberg DF, Gore JC, Zu Z. Accuracy in the quantification of chemical exchange saturation transfer (CEST) and relayed nuclear Overhauser enhancement (rNOE) saturation transfer effects. NMR Biomed 2017; [Crossref] [PubMed]
13. Zhou Y, Bie C, van Zijl PCM, Yadav NN. The relayed nuclear Overhauser effect in magnetization transfer and chemical exchange saturation transfer MRI. NMR Biomed 2022; Epub ahead of print. [Crossref] [PubMed]
14. Jones CK, Huang A, Xu J, Edden RA, Schär M, Hua J, Oskolkov N, Zacà D, Zhou J, McMahon MT, Pillai JJ, van Zijl PC. Nuclear Overhauser enhancement (NOE) imaging in the human brain at 7T. Neuroimage 2013;77:114-24. [Crossref] [PubMed]
15. Zhang XY, Xie J, Wang F, Lin EC, Xu J, Gochberg DF, Gore JC, Zu Z. Assignment of the molecular origins of CEST signals at 2 ppm in rat brain. Magn Reson Med 2017;78:881-7. [Crossref] [PubMed]
16. Liu Z, Yang Q, Luo H, Luo D, Qian L, Liu X, Zheng H, Sun PZ, Wu Y. Demonstration of fast and equilibrium human muscle creatine CEST imaging at 3 T. Magn Reson Med 2022;88:322-31. [Crossref] [PubMed]
17. Chung JJ, Jin T, Lee JH, Kim SG. Chemical exchange saturation transfer imaging of phosphocreatine in the muscle. Magn Reson Med 2019;81:3476-87. [Crossref] [PubMed]
18. Pavuluri K, Rosenberg JT, Helsper S, Bo S, McMahon MT. Amplified detection of phosphocreatine and creatine after supplementation using CEST MRI at high and ultrahigh magnetic fields. J Magn Reson 2020;313:106703. [Crossref] [PubMed]
19. Chen L, Schär M, Chan KWY, Huang J, Wei Z, Lu H, Qin Q, Weiss RG, van Zijl PCM, Xu J. In vivo imaging of phosphocreatine with artificial neural networks. Nat Commun 2020;11:1072. [Crossref] [PubMed]
20. Zhou Y, van Zijl PCM, Xu X, Xu J, Li Y, Chen L, Yadav NN. Magnetic resonance imaging of glycogen using its magnetic coupling with water. Proc Natl Acad Sci U S A 2020;117:3144-9. [Crossref] [PubMed]
21. van Zijl PC, Jones CK, Ren J, Malloy CR, Sherry AD. MRI detection of glycogen in vivo by using chemical exchange saturation transfer imaging (glycoCEST). Proc Natl Acad Sci U S A 2007;104:4359-64. [Crossref] [PubMed]
22. Simegn GL, Alhamud A, Robertson F, van der Kouwe AJW. Chemical Exchange Saturation Transfer MRI Optimal Continuous Wave RF Irradiation Parameters for Glycogen (glycoCEST) Detection. Appl Magn Reson 2020;51:621-40. [Crossref]
23. Yu L, Chen Y, Chen M, Luo X, Jiang S, Zhang Y, Chen H, Gong T, Zhou J, Li C. Amide Proton Transfer MRI Signal as a Surrogate Biomarker of Ischemic Stroke Recovery in Patients With Supportive Treatment. Front Neurol 2019;10:104. [Crossref] [PubMed]
24. Msayib Y, Harston GWJ, Tee YK, Sheerin F, Blockley NP, Okell TW, Jezzard P, Kennedy J, Chappell MA. Quantitative CEST imaging of amide proton transfer in acute ischaemic stroke. Neuroimage Clin 2019;23:101833. [Crossref] [PubMed]
25. Park JE, Jung SC, Kim HS, Suh JY, Baek JH, Woo CW, Park B, Woo DC. Amide proton transfer-weighted MRI can detect tissue acidosis and monitor recovery in a transient middle cerebral artery occlusion model compared with a permanent occlusion model in rats. Eur Radiol 2019;29:4096-104. [Crossref] [PubMed]
26. Cui J, Afzal A, Zu Z. Comparative evaluation of polynomial and Lorentzian lineshape-fitted amine CEST imaging in acute ischemic stroke. Magn Reson Med 2022;87:837-49. [Crossref] [PubMed]
27. Zhang XY, Wang F, Xu J, Gochberg DF, Gore JC, Zu Z. Increased CEST specificity for amide and fast-exchanging amine protons using exchange-dependent relaxation rate. NMR Biomed 2018; [Crossref] [PubMed]
28. Zhou IY, Lu D, Ji Y, Wu L, Wang E, Cheung JS, Zhang XA, Sun PZ. Determination of multipool contributions to endogenous amide proton transfer effects in global ischemia with high spectral resolution in vivo chemical exchange saturation transfer MRI. Magn Reson Med 2019;81:645-52. [Crossref] [PubMed]
29. Deshmane A, Zaiss M, Lindig T, Herz K, Schuppert M, Gandhi C, Bender B, Ernemann U, Scheffler K. 3D gradient echo snapshot CEST MRI with low power saturation for human studies at 3T. Magn Reson Med 2019;81:2412-23. [Crossref] [PubMed]
30. Zaiss M, Schmitt B, Bachert P. Quantitative separation of CEST effect from magnetization transfer and spillover effects by Lorentzian-line-fit analysis of z-spectra. J Magn Reson 2011;211:149-55. [Crossref] [PubMed]
31. Warnert EAH, Wood TC, Incekara F, Barker GJ, Vincent AJP, Schouten J, Kros JM, van den Bent M, Smits M, Tamames JAH. Mapping tumour heterogeneity with pulsed 3D CEST MRI in non-enhancing glioma at 3 T. MAGMA 2022;35:53-62. [Crossref] [PubMed]
32. Singh A, Debnath A, Cai K, Bagga P, Haris M, Hariharan H, Reddy R. Evaluating the feasibility of creatine-weighted CEST MRI in human brain at 7 T using a Z-spectral fitting approach. NMR Biomed 2019;32:e4176. [Crossref] [PubMed]
33. Chen Y, Dang X, Hu W, Sun Y, Bai Y, Wang X, He X, Wang M, Song X. Reassembled saturation transfer (REST) MR images at 2 B(1) values for in vivo exchange-dependent imaging of amide and nuclear Overhauser enhancement. Magn Reson Med 2023;89:620-35. [Crossref] [PubMed]
34. Chen Y, Dang X, Zhao B, Chen Z, Zhao Y, Zhao F, Zheng Z, He X, Peng J, Song X. Frequency importance analysis for chemical exchange saturation transfer magnetic resonance imaging using permuted random forest. NMR Biomed 2022; Epub ahead of print. [Crossref] [PubMed]
35. Zhou IY, Wang E, Cheung JS, Zhang X, Fulci G, Sun PZ. Quantitative chemical exchange saturation transfer (CEST) MRI of glioma using Image Downsampling Expedited Adaptive Least-squares (IDEAL) fitting. Sci Rep 2017;7:84. [Crossref] [PubMed]
36. Yao J, Ruan D, Raymond C, Liau LM, Salamon N, Pope WB, Nghiemphu PL, Lai A, Cloughesy TF, Ellingson BM. Improving B(0) Correction for pH-Weighted Amine Proton Chemical Exchange Saturation Transfer (CEST) Imaging by Use of k-Means Clustering and Lorentzian Estimation. Tomography 2018;4:123-37. [Crossref] [PubMed]
37. Arthur D, Vassilvitskii S. editors. k-means++: The Advantages of Careful Seeding. 18th ACM-SIAM Symposium on Discrete Algorithms; Jan 07-09, 2007; New Orleans, LA; 2007.
38. Cormen T, Leiserson C, Rivest R, Stein C. Breadth-first search. Introduction to Algorithms. MIT Press and McGraw-Hill; 1990:531-9.
39. Jones CK, Polders D, Hua J, Zhu H, Hoogduin HJ, Zhou J, Luijten P, van Zijl PC. In vivo three-dimensional whole-brain pulsed steady-state chemical exchange saturation transfer at 7 T. Magn Reson Med 2012;67:1579-89. [Crossref] [PubMed]
40. Kim M, Gillen J, Landman BA, Zhou J, van Zijl PC. Water saturation shift referencing (WASSR) for chemical exchange saturation transfer (CEST) experiments. Magn Reson Med 2009;61:1441-50. [Crossref] [PubMed]
41. Wang Z, Simoncelli EP, Bovik AC. editors. Multiscale structural similarity for image quality assessment. The Thrity-Seventh Asilomar Conference on Signals, Systems & Computers; Nov 9-12, 2003.
42. Cai K, Singh A, Poptani H, Li W, Yang S, Lu Y, Hariharan H, Zhou XJ, Reddy R. CEST signal at 2ppm (CEST@2ppm) from Z-spectral fitting correlates with creatine distribution in brain tumor. NMR Biomed 2015;28:1-8. [PubMed]
43. Di Bucchianico A. Coefficient of Determination (R2). Encyclopedia of Statistics in Quality and Reliability; 2008.
44. Welvaert M, Rosseel Y. On the definition of signal-to-noise ratio and contrast-to-noise ratio for FMRI data. PLoS One 2013;8:e77089. [Crossref] [PubMed]
45. Wu Y, Zhou IY, Lu D, Manderville E, Lo EH, Zheng H, Sun PZ. pH-sensitive amide proton transfer effect dominates the magnetization transfer asymmetry contrast during acute ischemia-quantification of multipool contribution to in vivo CEST MRI. Magn Reson Med 2018;79:1602-8. [Crossref] [PubMed]
46. Zong X, Wang P, Kim SG, Jin T. Sensitivity and source of amine-proton exchange and amide-proton transfer magnetic resonance imaging in cerebral ischemia. Magn Reson Med 2014;71:118-32. [Crossref] [PubMed]
47. Perlman O, Zhu B, Zaiss M, Rosen MS, Farrar CT. An end-to-end AI-based framework for automated discovery of rapid CEST/MT MRI acquisition protocols and molecular parameter quantification (AutoCEST). Magn Reson Med 2022;87:2792-810. [Crossref] [PubMed]
48. Kim B, Schär M, Park H, Heo HY. A deep learning approach for magnetization transfer contrast MR fingerprinting and chemical exchange saturation transfer imaging. Neuroimage 2020;221:117165. [Crossref] [PubMed]
49. Zhao Y, Wang X, Wang Y, Wang B, Zhang L, Wei X, He X. Application of a Markov chain Monte Carlo method for robust quantification in chemical exchange saturation transfer magnetic resonance imaging. Quant Imaging Med Surg 2022;12:5140-55. [Crossref] [PubMed]
50. Chen L, Barker PB, Weiss RG, van Zijl PCM, Xu J. Creatine and phosphocreatine mapping of mouse skeletal muscle by a polynomial and Lorentzian line-shape fitting CEST method. Magn Reson Med 2019;81:69-78. [Crossref] [PubMed]
51. Radke KL, Wilms LM, Frenken M, Stabinska J, Knet M, Kamp B, Thiel TA, Filler TJ, Nebelung S, Antoch G, Abrar DB, Wittsack HJ, Müller-Lutz A. Lorentzian-Corrected Apparent Exchange-Dependent Relaxation (LAREX) Ω-Plot Analysis-An Adaptation for qCEST in a Multi-Pool System: Comprehensive In Silico, In Situ, and In Vivo Studies. Int J Mol Sci 2022; [Crossref] [PubMed]
52. Bie C, Liang Y, Zhang L, Zhao Y, Chen Y, Zhang X, He X, Song X. Motion correction of chemical exchange saturation transfer MRI series using robust principal component analysis (RPCA) and PCA. Quant Imaging Med Surg 2019;9:1697-713. [Crossref] [PubMed]