Adiabatically prepared spin-lock could reduce the R_1ρ dispersion

Introduction

R_1ρ (=1/T_1ρ), the spin lattice relaxation rate in the rotating frame, has been used extensively to probe the relatively slow macromolecular processes, making it a practical tool for gaining information about water spin dynamics and interactions with endogenous macromolecules (1). Depending on the tissue types and the changes in tissue component and microenvironment, T_1ρ value may increase or decrease in diseases such as osteoarthritis (2-5), intervertebral disc degeneration (6,7), fibrosis (8,9), and liver steatosis (10,11). R_1ρ imaging involves the application of specific radiofrequency (RF) fields (called spin-lock fields) that can influence the R_1ρ relaxation processes so that the R_1ρ value varies with the strength of the RF pulse used. This dispersion of relaxation rate R_1ρ with the spin-lock field may be used to quantify the dynamic properties in biological tissues. There are different mechanisms potentially contributing to the R_1ρ relaxation, i.e., dipolar-dipolar interaction, diffusion, and chemical exchange (12-16). However, literature regarding R_1ρ relaxation mechanisms at 3T is somewhat inconsistent, with some groups reporting that similar to T₂, the dominating factor in T_1ρ relaxation is dipolar interaction (5,15,17,18), contrary to another study by Li et al. (19) where only a minor magic angle effect (associated with dipolar interaction) in cadaveric human femoral-tibial cartilage was observed. In addition, some studies reported that chemical exchange may be a main contributor to T_1ρ relaxation at high static fields (3T and above) and which leads to a significant T_1ρ dispersion in certain tissues (20-23). Based on the previous results (24-26), it was suggested that R_1ρ at very low locking fields (≤200 Hz) may reflect diffusion of tissue water molecules within field gradients caused by local magnetic field inhomogeneities, however, at higher locking fields, chemical exchange effects may dominate (14,27). Because the time scales of these two effects are so different, these two processes are readily separated (14). The dispersion of R_1ρ has been used to assess the vascular properties of muscles (14) and the water diffusion through susceptibility gradient in tumors (27); this was also used to characterize the contribution of chemical exchange from macromolecules that consist of labile protons (associated with hydroxyls, amides, amines) exchanging at an appropriate rate with the tissue water (20,25).

One of the challenges in R_1ρ imaging is that it is prone to artifacts arising from field inhomogeneities, which may greatly impact the R_1ρ quantification accuracy if not corrected. Previous studies have addressed the issues using different approaches, the commonly used approach is based on a composite block RF pulse clusters combining the rotary echo method (28) with a 180-degree refocusing pulse to compensate for the field imperfections (29), however the performance of the method relies on the perfection of the 180-degree pulse; another approach uses adiabatic pulses in the R_1ρ pre-pulse to tip down and back the magnetizations (30,31), which is termed “adiabatic prepared approach” in this paper to distinguish from the chains of adiabatic pulses used in (32,33). While both methods work well in terms of mitigating image artifacts, their influence on the dispersion degree has not been studied previously, with only one group showing that different image contrasts can be achieved by manipulating the pulse properties of the adiabatic and continuous-wave (CW) constant amplitude R_1ρ imaging experiments (32,33).

In our recent R_1ρ imaging in human knee cartilage, we observed that the degree of R_1ρ dispersion using the adiabatic approach (hyperbolic secant, HS1) was significantly lower than the block pulse approach. Prompted by this observation, we investigate whether and how the properties of tissue and RF pulses may influence the R_1ρ dispersion through numerical simulations. Although the current research progress on the origin of R_1ρ relaxation remain inconsistent, in this study we considered only the chemical exchange effect as its contribution appears to increase with the increasing static field as well as the locking field (20-22). We employed a two-pool model (the bulk water pool “a” and exchangeable solute pool “b”) and tracked the magnetization during the whole R_1ρ pre-pulse by solving the numerical solutions of the Bloch-McConnell equations (34). The R_1ρ values were computed exactly following the data fitting procedure in real applications, and the R_1ρ dispersion curves were extracted by plotting the R_1ρ values vs. spin-lock strengths. Specially, the simulations examined the dependencies of R_1ρ dispersion on (I) water pool fractional size P_a, (II) exchange rate from the solute to water pools, k_b, (III) the duration of the adiabatic pulse T_p, and (IV) chemical shift of the solute pool, ppm_b. We found that in general, with the increase of chemical exchange rate k_b, adiabatic pulse duration T_p, and chemical shift ppm_b, as well as the decrease of water pool size ratio P_a, the difference in R_1ρ dispersion between the block and adiabatic methods increasingly differs, with the R_1ρ dispersion curve of the adiabatic method becoming flatter. We present the following article in accordance with the MDAR reporting checklist (available at https://qims.amegroups.com/article/view/10.21037/qims-21-959/rc).

Methods

This study was conducted in accordance with the Declaration of Helsinki (as revised in 2013) and was approved by the local IRB (Institutional Review Board) and written informed consent was obtained from all participants.

Adiabatic pulse

Adiabatic pulse is both amplitude and frequency modulated. For the most prevalent hyperbolic secant (HS) family, the amplitude and frequency modulations have following forms:

w1(t)=w1maxsech((βtTp)n)[1]

Δw(t)=wRF(t)−w0=A∫sech2((βτTp)n)dτ[2]

where w1max is the maximum value of w₁(t), w₀ is the on-resonance frequency, w_RF is the carrier frequency of the pulse, T_p is the pulse duration, and A determines the amplitude of the frequency sweep, and β is a dimensionless truncation factor. One fundamental property of the adiabatic pulse is the time-bandwidth product given by:

TBW=Tp⋅BW[3]

where BW is the bandwidth of the pulse. With these definitions, the frequency sweep amplitude

A=π⋅BW=π⋅TBW/Tp[4]

When n=1, Eqs. [1] and [2] are simplified to the HS1 pulse:

w1(t)=w1maxsech(βTpt)[5]

Δw(t)=wRF(t)−w0=A∫sech2(βτTp)dτ=A⋅tanh(βTpt)[6]

The adiabatic condition is that the direction of effective magnetic field does not change much during one period of precession of the magnetization about the effective field. Under this condition, the adiabatic full passage pulse (AFP, one cycle of the hyperbolic secant function) is able to nutate the magnetization 180°, for instance, from z axis to -z axis despite of the RF inhomogeneity. One property of the adiabatic pulse is that the adiabatic half passage (AHP, half duration of the AFP) can turn the magnetization 90°.

Field inhomogeneities insensitive R_1ρ pre-pulse

In the typical spin-lock experiment, the equilibrium magnetization is nutated to the transverse plane by an RF pulse, the magnetization is then spin-locked by a continuous-wave constant amplitude spin-lock RF pulse for a period to generate the R_1ρ contrast, finally the magnetization is tipped back to the z-direction followed by signal acquisition. Figure 1 shows the R_1ρ imaging pulses that are commonly used to overcome artifacts from field inhomogeneities, details can be found in (29-31).

Figure 1 Diagram of the continuous-wave constant amplitude spin-lock pulse cluster to overcome field inhomogeneities. (A) Composite block R_1ρ pre-pulse. Magnetization is tipped a flip angle α_x about x axis by the first pulse, the spin-lock pulse (green box) is separated by a 180° refocusing pulse applied about the y axis at the middle of the spin-lock, forming two spin-lock segments with opposite phases (+y and -y). Finally, the R_1ρ prepared magnetization is turned back to -z axis by the second α_x pulse. (B) An AHP sequence is applied at the front of the R_1ρ pre-pulse to tip the magnetization a 90º, with the AM and FM derived from the HS1 pulse. The spin-lock pulse is applied with a duration of TSL and amplitude of FSL, at the end the rAHP pulse tips the magnetization back to the z axis. RF, radiofrequency; TSL, spin-lock time; AM, amplitude modulation; FM, frequency modulation; AHP, adiabatic half passage; HS1, hyperbolic secant (n=1); FSL, spin-lock frequency; rAHP, reverse AHP.

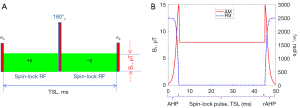
Previous observation

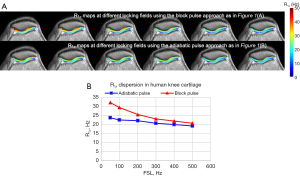
Previous study used R_1ρ dispersion to assess chemical exchange in knee cartilage with the R_1ρ pulse as in Figure 1A, significant dispersion was observed for a spin-lock frequency range from 0 to 550 Hz on a Philips 3T Achieva scanner (Philips Healthcare, Cleveland, OH, USA) (20). However, in our later experiments with the adiabatic approach as in Figure 1B on healthy volunteers (n=3), only negligible dispersion was found, see Figure 2, which prompts us to study whether the properties of the tissue and pulse affect the dispersion degree.

Figure 2 R_1ρ imaging in human knee cartilage. (A) R_1ρ map in knee cartilage at different locking fields for block (upper row) and adiabatic (lower row) pulses as in Figure 1. Left to right corresponds to the FSL = [50, 100, 200, 300, 400, 500] Hz. For the block pulse approach, TSL = [2, 22, 42, 62, 82] ms; for the adiabatic pulse approach, TSL = [1, 21, 41, 61, 81] ms. Other parameters: FOV =148×128 mm², matrix size =320×320, thickness =4 mm. Data were acquired by the Turbo Spin Echo sequence. (B) R_1ρ dispersion from the knee cartilage, median values of R_1ρ were used in the plot. FSL, spin-lock frequency; TSL, spin-lock time; FOV, field of view.

Numerical simulations

We only investigate the chemical exchange effect on R_1ρ relaxation in the simulations. We examine whether the dispersion of the block and adiabatic methods behaves differently to the properties of tissue and the RF at the main magnetic field of 3.0T. We assume a two-pool exchange tissue model, i.e., the bulk water pool “a” and a smaller metabolite pool “b” with certain chemical shift and exchange rate. The behavior of this two-pool exchanging system may be analyzed using the Bloch-McConnell equations as below (34):

ddt=(MxaMxbMyaMybMzaMzb)=(−R2a−kakbΔw0a−w1z0−w1y0ka−R2b−kb0Δw0b−w1z0−w1y−Δw2a−w1z0−R2a−kakbw1x00−Δw0b−w1zka−R2b−kb0w1xw1y0−w1x0−R1a−kakb0w1y0−w1xka−R1b−kb)⋅(MxaMxbMyaMybMzaMzb)+(0000R1aM0aR1bM0b)[7]

where Mx,y,za,b denotes the magnetization along x (or y, z) axis for pool a and pool b, M0a,b is the equilibrium magnetization of pool a or b, R1,2a,b the longitudinal (or transverse) relaxation rate for the two pools; k_a and k_b are chemical exchange rates from pool a to pool b, and from pool b to pool a respectively. In addition, w1x,1y,1z describes the applied RF field in x (or y, z) axis respectively, and Δw0a,b is the chemical shift terms for pool a or b. Finally, the pool fractional size is defined as P_a and P_b, with P_a + P_b =1, and also k_a = (k_b · P_b)/P_a.

The numerical solutions of the Bloch-McConnell equations were obtained using Matlab (Mathworks, R2018a) codes by solving the ordinary differential equations, the magnetizations were tracked from excitation to reversion during the R_1ρ pre-pulse, exactly following the real R_1ρ experiments. The MRI signals (the final magnetizations that have been turned to z axis) were fitted to a two-parameter mono-exponential model

S=S0⋅exp(−TSL⋅R1ρ)[8]

We mainly focus on whether the tissue and RF properties affect the dispersion for the block and adiabatic methods, so the field inhomogeneities were not considered in the simulations. An AHP HS1 pulse (Eqs. [5] and [6]) was selected for the adiabatic method, with β =4.0, TBW =10, and w1max=2π⋅γ⋅B1max (γ is the gyromagnetic ratio 42.58×10⁶ Hz/Tesla, and B1max=15.0μT is the maximum B₁ assumed at 3T), the frequency sweep amplitude A can be derived from Eq. [4]. The experiments were performed with a series of TSLs {=[0, 20, 40, 60] ms} and FSLs from 50 to 1,000 Hz with an increment of 25 Hz. The dispersion curves of both methods were compared under varied values of P_a, k_b, T_p (AHP HS1 pulse duration), and ppm_b (pool b chemical shift). Since the block pulse duration is almost always chosen for the shortest value (<2 ms), its effect was not considered in the simulations.

To investigate how the parameters (P_a, k_b, T_p, ppm_b) affect R_1ρ dispersion, four situations were considered and for each scenario one of the four parameters was treated as a variable within a certain range while the other three parameters remained fixed but with two options: a low and a high value, which led to eight subcases for each situation. Specifically, the simulations were organized as below: (I) P_a varies from 0.80 to 0.95, k_b =2,000 or 500 Hz, T_p =10 or 25 ms, and ppm_b =1.0 or 5.0 ppm; (II) k_b varies from 500 to 3,000 Hz, P_a =0.95 or 0.80, T_p =10 or 25 ms, and ppm_b =1.0 or 5.0 ppm; (III) T_p varies from 5.0 to 25 ms, P_a =0.95 or 0.80, k_b =2,000 or 500 Hz, and ppm_b =1.0 or 5.0 ppm; (IV) ppm_b varies from 1.0 to 5.0 ppm, P_a =0.95 or 0.80, k_b =2,000 or 500 Hz, and T_p =10 or 25 ms.

Results

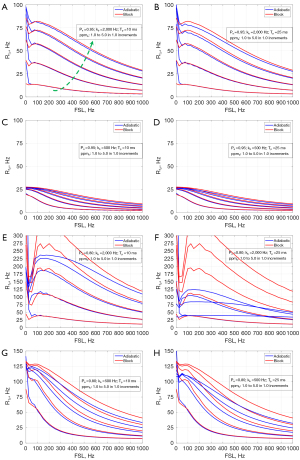
Figure 3 shows the comparisons of R_1ρ dispersion between the block and adiabatic methods, for a series of P_a (0.80 to 0.95 in 0.05 increments) and various combinations of k_b (500 vs. 2,000 Hz), T_p (10 vs. 25 ms), and ppm_b (1.0 vs. 5.0 ppm). It is seen that for different k_b and T_p, the dispersion curves between the block and AHP methods largely match well for the range of P_a at the small ppm_b of 1.0 (Figure 3A,3C,3E,3G), though T_p =25 ms appears to have greater error (Figure 3C,3G). However, with a large ppm_b = 5.0, the dispersion curves increasingly differ with the decrease of P_a (Figure 3B,3D,3F,3H), the difference becomes more evident at large T_p than at short T_p (Figure 3D vs. Figure 3B, and Figure 3H vs. Figure 3F). Also, the dispersion curves of the adiabatic method appear much flatter at large ppm_b and T_p (Figure 3D).

Figure 3 Comparison of R_1ρ dispersion using adiabatic pulses vs. block pulses for excitation and reversion. The simulation parameters are T_1a =4,000 ms, T_2a =2,000 ms, T_1b =1,250 ms. T_2b =35 ms, TSL = [0, 20, 40, 60] ms, FSL = 0 to 1,000 Hz with an increment of 25 Hz. The parameters k_b, T_p, and ppm_b are specified in (A) – (H), where the comparison is performed for a range of P_a values [0.80, 0.85, 0.90, 0.95]. The curved arrow in (A) shows the direction of P_a increase, which is applicable to other subfigures (B) – (H). TSL, spin-lock time; FSL, spin-lock frequency.

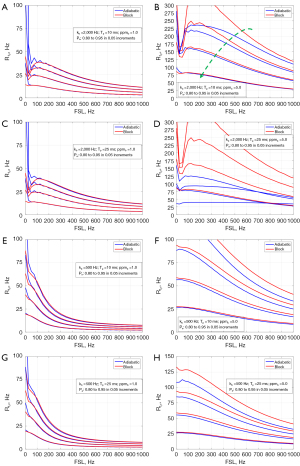
Figure 4 shows the comparisons of R_1ρ dispersion for a range of k_b (500 to 3,000 Hz in 500 increments), with the combination of P_a (0.80 vs. 0.95), T_p (10 vs. 25 ms), and ppm_b (1.0 vs. 5.0). Generally, the dispersion curves of the two methods are well close at the small ppm_b = 1.0 (Figure 4A,4C,4E,4G). At the large ppm_b =5.0, a small P_a (=0.80) can cause a large difference between the dispersion curves for both the pulse durations (Figure 4F,4H).

Figure 4 Comparison of R_1ρ dispersion using adiabatic pulses vs. block pulses for excitation and reversion. The simulation parameters are T_1a =4,000 ms, T_2a =2,000 ms, T_1b =1,250 ms. T_2b =35 ms, TSL = [0, 20, 40, 60] ms, FSL = 0 to 1,000 Hz with an increment of 25 Hz. The parameters P_a, T_p, and ppm_b are specified in (A) – (H), where the comparison is performed for a range of k_b values [500, 1,000, 1,500, 2,000, 2,500, 3,000] Hz. The curved arrow in (A) shows the direction of k_b increase, which is applicable to other subfigures (B) – (H). TSL, spin-lock time; FSL, spin-lock frequency.

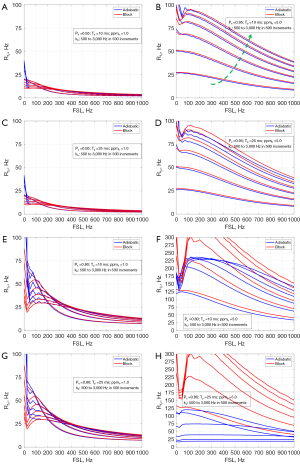
Figure 5 demonstrates the comparisons with a range of T_p (5.0 to 25 ms in 5.0 increments) under different combinations of P_a (0.80 vs. 0.95), k_b (500 vs. 3,000 Hz), and ppm_b (1.0 vs. 5.0). For all situations, the dispersion curves between the two methods match very well except for the case with P_a =0.80, k_b=2,000 Hz, and ppm_b =5.0, see Figure 5F, where the difference increases with the pulse duration T_p.

Figure 5 Comparison of R_1ρ dispersion using adiabatic pulses vs. block pulses for excitation and reversion. The simulation parameters are T_1a =4,000 ms, T_2a =2,000 ms, T_1b =1,250 ms. T_2b =35 ms, TSL = [0, 20, 40, 60] ms, FSL =0 to 1,000 Hz with an increment of 25 Hz. The parameters P_a, k_b, and ppm_b are specified in (A) – (H), where the comparison is performed for a range of T_p values [5, 10, 15, 20, 25] ms. The curved arrow in (A) shows the direction of T_p increase, which is applicable to other subfigures (B) – (H). For the block pulse method, the shortest pulse duration is always used so there is only one curve for the block pulse method in each of the subfigure. TSL, spin-lock time; FSL, spin-lock frequency.

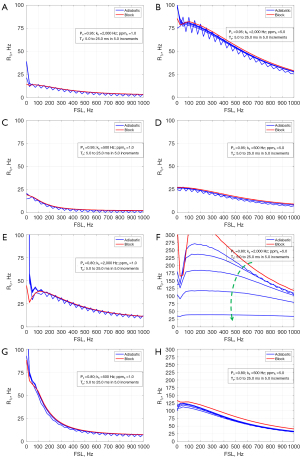
Finally, Figure 6 shows the situation for a range of ppm_b (1.0 to 5.0 in 1.0 increment) and different combinations of P_a (0.80 vs. 0.95), k_b (500 vs. 2,000 Hz), and T_p (10 vs. 25 ms). It shows that at small P_a (=0.80), the dispersion difference between the two methods tends to increase but a large k_b (=2,000 Hz) and large ppm_b (=5.0) exacerbate the difference, see Figure 6E,6F, in which the dispersion of the adiabatic approach appears flatter.

Figure 6 Comparison of R_1ρ dispersion using adiabatic pulses vs. block pulses for excitation and reversion. The simulation parameters are T_1a =4,000 ms, T_2a =2,000 ms, T_1b =1,250 ms. T_2b =35 ms, TSL = [0, 20, 40, 60] ms, FSL =0 to 1,000 Hz with an increment of 25 Hz. The parameters P_a, k_b, and T_p are specified in (A) – (H), where the comparison is performed for a range of ppm_b values [1.0, 2.0, 3.0, 4.0, 5.0]. The curved arrow in (A) shows the direction of ppm_b increase, which is applicable to other subfigures (B) – (H). TSL, spin-lock time; FSL, spin-lock frequency.

Discussion

R_1ρ dispersion holds great potential to assess molecular dynamics in biological tissues and has been exploited as an important method for the early diagnosis of diseases. Although other mechanisms such as dipolar effect and diffusion may contribute, previous studies reported that chemical exchange may be a main contributor to the R_1ρ dispersion at higher magnetic fields (14,15,20,21). Exploiting the R_1ρ dispersion holds great potential for the characterization of tissue composition and the physicochemical changes associated with pathology.

In this study, we investigated the difference of R_1ρ dispersion between the block and adiabatic methods under solely the effect of chemical exchange at 3T using a two-pool model system. We considered the influence of different parameters of pool size P_a, chemical exchange rate k_b, adiabatic pulse duration T_p, and the chemical shift of the solute pool ppm_b. It is seen that generally, the larger ppm_b, k_b, and T_p, and the smaller P_a, the more pronounced difference in the R_1ρ dispersion between the block and adiabatic methods, with the dispersion curve of the adiabatic method appears flatter. Although the dispersion difference is determined by the combination of these parameters, it seems that ppm_b is a more sensitive factor. In contrast, the smaller ppm_b, k_b, and T_p, and the greater P_a, the better coincidence between the two methods.

This study has several limitations. First, wider ranges of parameter were used in the simulations to better reveal the effect of the parameter on the R_1ρ dispersion, so the dispersion curves in some scenarios might look different from those observed in biological tissues (in scale and/or pattern). Second, only chemical exchange was considered and the readout sequence was neglected. In the real R_1ρ experiment in biological tissues, however, other relaxation channels such as diffusion, dipolar-dipolar interaction may also contribute to the R_1ρ dispersion. Also depending on the readout sequence, the R_1ρ contrast may be compromised by the relaxation parameters and pulse sequence parameters (35). Third, this study was based on simulations only, however, systematically designed real experiments would be essential in the validation of the theoretical analysis and simulations. Our future work will focus more on the investigation of R_1ρ relaxation mechanisms and their validation. Nevertheless, the simulations showed that at certain conditions, the adiabatic pulse method may lead to significantly lower R_1ρ dispersion than the block pulse approach, as we have observed in knee cartilage imaging (Figure 2), suggesting that care should be taken when using adiabatic approach to study the R_1ρ dispersion. The difference in R_1ρ dispersion between the two approaches may be because the tipping pulses (adiabatic vs. block) have different effect on the magnetizations, and the effect depends on the properties of both the tipping pulses and tissues.

Previous R_1ρ studies in cartilage mainly focused on whether R_1ρ values are relevant to the concentration of glycosaminoglycan (GAG), a side chain of proteoglycan and clinically an indication of osteoarthritis, although there have been conflicting conclusions regarding the origins of the R_1ρ contrast (3,5,36-38). There were very few studies investigating the effect of both proteoglycan and collagen on R_1ρ values in cartilage specimens, with one study concluding that degradation of proteoglycans and collagen fibers in the articular cartilage increased the articular cartilage T_1ρ (=1/R_1ρ) value (39), and another study being that T_1ρ may be primarily determined by collagen concentration but the molecular level interactions associated with collagen/GAG may be contributing in an important way to T_1ρ (4). In our early study of R_1ρ dispersion in knee cartilage with the block pulse approach (20), we speculated that the chemical exchange was mainly between free water and hydroxyls in GAGs. Since the chemical shift of hydroxyls is small about 1.0–1.2 ppm, it may not account for the difference of the R_1ρ curves for the block and adiabatic methods (Figure 2). According to the simulations in our paper, the important reason causing the dispersion difference would be the large chemical shift ppm_b, which perhaps suggests that other substance in the cartilage, for instance the most abundant collagens, may also participate in the chemical exchange process, as the collagen macromolecules have exchangeable amine and amide protons (40) with large chemical shifts (amide NH: 5.5–8 ppm, and amine NH₂: 0.5–3.0 ppm) (41). This interpretation differs from some previous conclusions about the chemical exchange in knee cartilage.

We observed a “dip” sometimes occurring at the lower FSLs (for instance <100 Hz) in Figures 3-6, which we have also observed sometimes in the real R_1ρ experiments in biological tissues. We interpret this as a situation where the spins are not “locked” efficiently about the locking field direction at lower locking fields, the “dip” is generally less prominent at large water pool size P_a, small exchange rate k_b, and small chemical shift of the bound pool ppm_b.

Conclusions

In conclusion, it is suggested that care should be taken when using the adiabatically prepared approach to study R_1ρ dispersion. The adiabatic approach may compromise the R_1ρ dispersion, the effect is determined by the combination of the tissue and RF properties.

Acknowledgments

Funding: This work was supported by the Barrow Neurological Foundation (No. 455003033568).

Footnote

Reporting Checklist: The author has completed the MDAR reporting checklist. Available at https://qims.amegroups.com/article/view/10.21037/qims-21-959/rc

Conflicts of Interest: The author has completed the ICMJE uniform disclosure form (available at https://qims.amegroups.com/article/view/10.21037/qims-21-959/coif). The author has no conflicts of interest to declare.

Ethical Statement: The author is accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). The study was approved by the local IRB (Institutional Review Board) and written informed consent was obtained from all participants.

Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.

References

1. Liepinsh E, Otting G. Proton exchange rates from amino acid side chains--implications for image contrast. Magn Reson Med 1996;35:30-42. [Crossref] [PubMed]
2. Borthakur A, Mellon E, Niyogi S, Witschey W, Kneeland JB, Reddy R. Sodium and T1rho MRI for molecular and diagnostic imaging of articular cartilage. NMR Biomed 2006;19:781-821. [Crossref] [PubMed]
3. Li X, Benjamin Ma C, Link TM, Castillo DD, Blumenkrantz G, Lozano J, Carballido-Gamio J, Ries M, Majumdar S. In vivo T(1rho) and T(2) mapping of articular cartilage in osteoarthritis of the knee using 3 T MRI. Osteoarthritis Cartilage 2007;15:789-97. [Crossref] [PubMed]
4. Menezes NM, Gray ML, Hartke JR, Burstein D. T2 and T1rho MRI in articular cartilage systems. Magn Reson Med 2004;51:503-9. [Crossref] [PubMed]
5. Mlynárik V, Szomolányi P, Toffanin R, Vittur F, Trattnig S. Transverse relaxation mechanisms in articular cartilage. J Magn Reson 2004;169:300-7. [Crossref] [PubMed]
6. Paul CPL, Smit TH, de Graaf M, Holewijn RM, Bisschop A, van de Ven PM, Mullender MG, Helder MN, Strijkers GJ. Quantitative MRI in early intervertebral disc degeneration: T1rho correlates better than T2 and ADC with biomechanics, histology and matrix content. PLoS One 2018;13:e0191442. [Crossref] [PubMed]
7. Wáng YX, Zhang Q, Li X, Chen W, Ahuja A, Yuan J. T1ρ magnetic resonance: basic physics principles and applications in knee and intervertebral disc imaging. Quant Imaging Med Surg 2015;5:858-85. [PubMed]
8. Hectors SJ. Is MRI relaxometry parameter T1ρ specific to fibrosis or confounded by concomitant pathological features? Quant Imaging Med Surg 2020;10:2408-10. [Crossref] [PubMed]
9. Wang F, Colvin DC, Wang S, Li H, Zu Z, Harris RC, Zhang MZ, Gore JC. Spin-lock relaxation rate dispersion reveals spatiotemporal changes associated with tubulointerstitial fibrosis in murine kidney. Magn Reson Med 2020;84:2074-87. [Crossref] [PubMed]
10. Zhao F, Zhou N, Wang X, Wang JL, Zhong WX, Deng M, Zheng CJ, He J, Yan SX, Wáng YXJ. T1rho shortening effect of fat in liver steatosis after fat suppression: approximate estimation in a methionine and choline-deficient (MCD) diet rat model. Quant Imaging Med Surg 2021;11:870-5. [Crossref] [PubMed]
11. Okuaki T, Takayama Y, Nishie A, Ogino T, Obara M, Honda H, Miyati T, Van Cauteren M. T1ρ mapping improvement using stretched-type adiabatic locking pulses for assessment of human liver function at 3T. Magn Reson Imaging 2017;40:17-23. [Crossref] [PubMed]
12. Akella SV, Regatte RR, Wheaton AJ, Borthakur A, Reddy R. Reduction of residual dipolar interaction in cartilage by spin-lock technique. Magn Reson Med 2004;52:1103-9. [Crossref] [PubMed]
13. Cobb JG, Xie J, Gore JC. Contributions of chemical and diffusive exchange to T1ρ dispersion. Magn Reson Med 2013;69:1357-66. [Crossref] [PubMed]
14. Adelnia F, Zu Z, Spear JT, Wang F, Harkins KD, Gore JC. Tissue characterization using R1rho dispersion imaging at low locking fields. Magn Reson Imaging 2021;84:1-11. [Crossref] [PubMed]
15. Shao H, Pauli C, Li S, Ma Y, Tadros AS, Kavanaugh A, Chang EY, Tang G, Du J. Magic angle effect plays a major role in both T1rho and T2 relaxation in articular cartilage. Osteoarthritis Cartilage 2017;25:2022-30. [Crossref] [PubMed]
16. Pang Y, Palmieri-Smith RM, Malyarenko DI, Swanson SD, Chenevert TL. A unique anisotropic R2 of collagen degeneration (ARCADE) mapping as an efficient alternative to composite relaxation metric (R2 -R1ρ) in human knee cartilage study. Magn Reson Med 2019;81:3763-74. [Crossref] [PubMed]
17. Du J, Statum S, Znamirowski R, Bydder GM, Chung CB. Ultrashort TE T1ρ magic angle imaging. Magn Reson Med 2013;69:682-7. [Crossref] [PubMed]
18. Mlynárik V, Trattnig S, Huber M, Zembsch A, Imhof H. The role of relaxation times in monitoring proteoglycan depletion in articular cartilage. J Magn Reson Imaging 1999;10:497-502. [Crossref] [PubMed]
19. Li X, Cheng J, Lin K, Saadat E, Bolbos RI, Jobke B, Ries MD, Horvai A, Link TM, Majumdar S. Quantitative MRI using T1ρ and T2 in human osteoarthritic cartilage specimens: correlation with biochemical measurements and histology. Magn Reson Imaging 2011;29:324-34. [Crossref] [PubMed]
20. Wang P, Block J, Gore JC. Chemical exchange in knee cartilage assessed by R1ρ (1/T1ρ) dispersion at 3T. Magn Reson Imaging 2015;33:38-42. [Crossref] [PubMed]
21. Spear JT, Gore JC. New insights into rotating frame relaxation at high field. NMR Biomed 2016;29:1258-73. [Crossref] [PubMed]
22. Cobb JG, Xie J, Gore JC. Contributions of chemical exchange to T1ρ dispersion in a tissue model. Magn Reson Med 2011;66:1563-71. [Crossref] [PubMed]
23. Chopra S, McClung R, Jordan R. Rotating-frame relaxation rates of solvent molecules in solutions of paramagnetic ions undergoing solvent exchange. J Magn Reson 1984;59:361-72.
24. Cobb JG, Li K, Xie J, Gochberg DF, Gore JC. Exchange-mediated contrast in CEST and spin-lock imaging. Magn Reson Imaging 2014;32:28-40. [Crossref] [PubMed]
25. Cobb JG, Xie J, Li K, Gochberg DF, Gore JC. Exchange-mediated contrast agents for spin-lock imaging. Magn Reson Med 2012;67:1427-33. [Crossref] [PubMed]
26. Spear JT, Zu Z, Gore JC. Dispersion of relaxation rates in the rotating frame under the action of spin-locking pulses and diffusion in inhomogeneous magnetic fields. Magn Reson Med 2014;71:1906-11. [Crossref] [PubMed]
27. Zu Z, Janve V, Gore JC. Spin-lock imaging of intrinsic susceptibility gradients in tumors. Magn Reson Med 2020;83:1587-95. [Crossref] [PubMed]
28. Charagundla SR, Borthakur A, Leigh JS, Reddy R. Artifacts in T(1rho)-weighted imaging: correction with a self-compensating spin-locking pulse. J Magn Reson 2003;162:113-21. [Crossref] [PubMed]
29. Witschey WR 2nd, Borthakur A, Elliott MA, Mellon E, Niyogi S, Wallman DJ, Wang C, Reddy R. Artifacts in T1 rho-weighted imaging: compensation for B(1) and B(0) field imperfections. J Magn Reson 2007;186:75-85. [Crossref] [PubMed]
30. Chen W. Artifacts correction for T1rho imaging with constant amplitude spin-lock. J Magn Reson 2017;274:13-23. [Crossref] [PubMed]
31. Schuenke P, Koehler C, Korzowski A, Windschuh J, Bachert P, Ladd ME, Mundiyanapurath S, Paech D, Bickelhaupt S, Bonekamp D, Schlemmer HP, Radbruch A, Zaiss M. Adiabatically prepared spin-lock approach for T1ρ-based dynamic glucose enhanced MRI at ultrahigh fields. Magn Reson Med 2017;78:215-25. [Crossref] [PubMed]
32. Mangia S, Liimatainen T, Garwood M, Michaeli S. Rotating frame relaxation during adiabatic pulses vs. conventional spin lock: simulations and experimental results at 4 T. Magn Reson Imaging 2009;27:1074-87. [Crossref] [PubMed]
33. Michaeli S, Sorce DJ, Garwood M. T2rho and T1rho Adiabatic Relaxations and Contrasts. Curr Anal Chem 2008;4:8-25. [Crossref]
34. McConnell HM. Reaction rates by nuclear magnetic resonance. J Chem Phys 1958;28:430-1. [Crossref]
35. Chen W. Errors in quantitative T1rho imaging and the correction methods. Quant Imaging Med Surg 2015;5:583-91. [PubMed]
36. Son M, Goodman SB, Chen W, Hargreaves BA, Gold GE, Levenston ME. Regional variation in T1ρ and T2 times in osteoarthritic human menisci: correlation with mechanical properties and matrix composition. Osteoarthritis Cartilage 2013;21:796-805. [Crossref] [PubMed]
37. van Tiel J, Kotek G, Reijman M, Bos PK, Bron EE, Klein S, Nasserinejad K, van Osch GJ, Verhaar JA, Krestin GP, Weinans H, Oei EH. Is T1ρ Mapping an Alternative to Delayed Gadolinium-enhanced MR Imaging of Cartilage in the Assessment of Sulphated Glycosaminoglycan Content in Human Osteoarthritic Knees? An in Vivo Validation Study. Radiology 2016;279:523-31. [Crossref] [PubMed]
38. Regatte RR, Akella SV, Lonner JH, Kneeland JB, Reddy R. T1rho relaxation mapping in human osteoarthritis (OA) cartilage: comparison of T1rho with T2. J Magn Reson Imaging 2006;23:547-53. [Crossref] [PubMed]
39. Choi WS, Yoo HJ, Hong SH, Choi JY. The Effects of Proteoglycan and Type II Collagen on T1ρ Relaxation Time of Articular Cartilage. J Korean Soc Radiol 2015;72:108-14. [Crossref]
40. Book. Cartilage Imaging: Significance, Techniques, and New Developments. Springer, 2011.
41. Webpage. Available online: https://tigerweb.towson.edu/jdiscord/www/paperwork_fall2018/labinfofall2018/spectroscopyvalues.pdf, accessed October 20 2022.