
Distribution and regional variation of wall shear stress in the curved middle cerebral artery using four-dimensional flow magnetic resonance imaging
Introduction
Hemodynamic factors have been shown to play an important role in the formation and development of vascular diseases, including atherosclerosis (AS), aneurysms, and arteriovenous malformations (AVMs) (1-3). Irregular vascular geometry, including bifurcation, curvature, and branching, can lead to regionally different flow status, which subsequently generates spatial and temporal changes in the shear forces acting on a vessel wall. As a key parameter in cardiovascular hemodynamics, wall shear stress (WSS) (4) expresses the force per unit area exerted by the wall on the blood flow in a direction on the local tangent plane, which is linked to the initiation and progression of many vascular diseases (5-7). The oscillatory shear index (OSI) is a WSS-related parameter that describes the WSS directional changes during the cardiac cycle. It has been well accepted that low WSS and a high OSI represent sensitive markers for the formation of atherosclerotic plaques (8). Previous studies of the aorta, carotid, and coronary arteries have shown that atherosclerotic plaques develop preferentially at curved arteries and near side branches, which are in the regions exposed to disturbed flow and shear stress (9-12).
The proximal (M1) segment of the middle cerebral artery (MCA), which extends from the ending of the internal carotid artery to the first main division of the MCA, is one of the most common locations of intracranial atherosclerotic plaques (13). Although the M1 segment (also termed the horizontal segment) is generally considered straight, it has a curved shape in many cases. Several studies have reported that the MCA geometry is associated with plaque distribution and stroke (14,15). It has been indicated that MCA plaques are preferentially located on the inner wall of the curved MCA (15). One study using computational fluid dynamics (CFD) showed that AS might occur in the middle of a branch of the MCA with the highest geometrical curvature (16). The possible explanation was that the curved MCA affected local hemodynamic status, resulting in the uneven distribution of WSS on the circumferential plane of the curved MCA. However, to date, few hemodynamic studies have measured the distribution of WSS on the curved MCA in vivo before the development of AS.
Four-dimensional (4D) flow magnetic resonance imaging (MRI), which shows the real-time blood flow patterns of individual patients, allows for the in vivo quantification and comprehensive assessment of the cardiovascular system. Using this technique, volumetric velocity data can be directly obtained in a three-dimensional (3D) direction during a cardiac cycle period (17). After the flow data are processed, noninvasive qualitative and quantitative assessments can be accurately performed on flow velocity and other hemodynamic parameters, including flow rate, WSS, and pressure, during the entire cardiac cycle. Using this technique, in vivo studies have been conducted on patients with congenital heart disease, aorta dilation, and extracranial-intracranial bypass, with favorable and promising results demonstrated (18-20). The reproducibility of this technique has also been verified in previous studies (21,22).
We hypothesized that WSS parameters may be different among the 3 different sections (proximal, curved, and distal) of the long axis of the M1 segment of the curved MCA, and the curved M1 may have a certain shear force spatial distribution at the most curved location. The purpose of this study was to investigate the distribution and regional variation of the WSS of curved MCAs using 4D flow imaging in healthy participants. We present the following article in accordance with the Strengthening the Reporting of Observational Studies in Epidemiology (STROBE) reporting checklist (available at https://qims.amegroups.com/article/view/10.21037/qims-22-67/rc).
Methods
Participants
This cross-sectional study enrolled 49 healthy participants from Beijing Tiantan Hospital between May 2016 to November 2020. Individuals were excluded if they had cardiovascular diseases, a history of central nervous system diseases, or vascular risk factors such as hypertension, hyperlipemia, diabetes, smoking, and drinking. Those with claustrophobia or contraindication for MRI examination or scans of poor image quality were also excluded. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013) and supported by the Institutional Review Board of Beijing Tiantan Hospital, Capital Medical University (No. KY 2019-053-02). Written informed consent was provided by all study participants.
MRI and flow data acquisition
The MRIs were carried out with 3.0 Tesla MR scanners (Trio Tim, Siemens, Erlangen, Germany; Ingenia CX, Philips Healthcare, Best, the Netherlands) with a 32-channel head coil. A 3D time-of-flight (TOF) magnetic resonance angiography (MRA) was performed with maximum intensity projection (MIP) reconstruction to visualize the morphology of the intracranial arteries. Then, 4D flow data were acquired with an oblique coronal orientation, covering the M1 and M2 segments of MCAs, bilaterally. The 4D flow imaging was carried out using the standard generalized autocalibrating partial parallel acquisition (GRAPPA) parallel imaging for the Siemens MR scanner and the accelerated compressed sensing (CS) 4D flow MRI for the Philips MR scanner. All flow data were acquired using prospective and pulse gating, and the scan time was 8–13 min, depending on the heartbeats of the participants. The parameters of the imaging sequences are listed in Table 1.
Table 1
| Parameters | Siemens | Philips | |||
|---|---|---|---|---|---|
| 3D TOF MRA | 4D flow MRI | 3D TOF MRA | 4D flow MRI | ||
| TR/TE (ms) | 22/3.5 | 54.96/3.13 | 21/3.4 | 8.7/4.1 | |
| Flip angle (°) | 18 | 15 | 17 | 20 | |
| Field of view (mm2) | 200×200 | 200×140 | 200×200 | 160×160 | |
| Matrix size | 384×250 | 208×140 | 384×250 | 160×160 | |
| Slice thickness (mm) | 1.3 | 1.0 | 1.3 | 1.0 | |
| Slices | 120 | 36 | 120 | 36 | |
| Acceleration factor | 2 | 2 | 2 | 3 | |
| In-plane resolution (mm2) | 0.52×0.8 | 1.0×1.0 | 0.52×0.8 | 1.0×1.0 | |
| Venc (cm/s) | – | 120 | – | 120 | |
| Scan time (min) | 2–3 | 11–13 | 2–3 | 8–10 | |
MRA, magnetic resonance angiography; 3D TOF MRA, three-dimensional time-of-flight magnetic resonance angiography; 4D flow MRI, four-dimensional flow magnetic resonance imaging; TR, repetition time; TE, echo time; Venc, velocity encoding.
Definition of the curved M1 segment and the cross-sectional plane setting
According to the vessel projections on the MIP images of the 3D TOF MRA, the shape of the M1 segment was classified into 3 groups according to a previous study (23): (I) straight; (II) C-shaped; and (III) S-shaped MCA. In order to reduce the influence due to morphological differences of the other 2 types of arteries, only the C-shaped MCA, called the curved MCA, was included and analyzed in this study. On the coronal and axial MRA MIP images, 2 straight lines were drawn through the midline of the target MCA, 1 from the ICA termination (a’) to the most curved point (c’) and the other from the MCA bifurcation (b’) to the most curved point (c’) (24). If the intersection angle of these 2 straight lines was larger than 10° on the coronal or axial MRA MIP images, the vessel was defined as a curved-shaped M1 vessel (Figure 1).
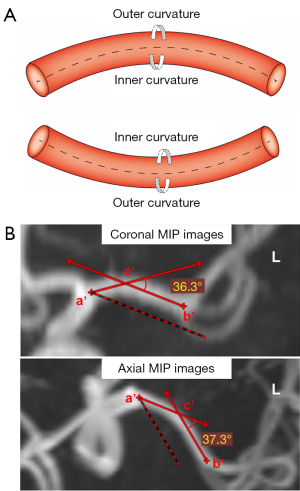
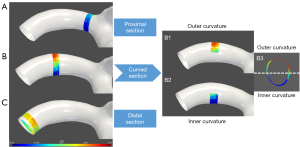
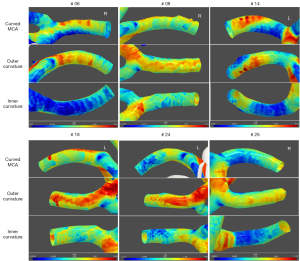
For each artery, 3 cross-sectional planes with a thickness of 1 mm perpendicular to the long axis of the curved M1 segment were selected and analyzed. The planes were set 1 mm at the distal end of the beginning of the M1 segment (proximal section) and 1 mm before the M2 bifurcation (distal section), respectively. The curved M1 section was selected at the most curved point. As for the curved M1 section, the circumferential wall was divided and described as the inner curvature and outer curvature of the curved MCA, according to the opening orientation of the curved M1 segment (15), as shown in Figure 2. Then, the planes perpendicular and parallel to the opening orientation were defined separately. The inner curvature and outer curvature were divided along the perpendicular line through the cross-sectional plane. The curved-shaped M1, the curved M1 section, and the inner/outer curvature were independently defined by two observers (Dr. B.X. and Dr. F.M.), and the differences between the two observers were solved by consensus.
Postprocessing and 3D visualization of 4D flow data
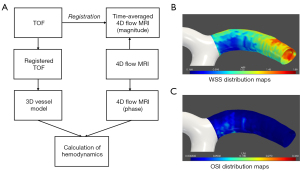
The time-average images of the 4D flow MRI were obtained by MATLAB software (The MathWorks, Natick, MA, USA). The TOF MRA MIP images were used for vessel wall segmentation due to the better blood flow signal contrast. The TOF MRA images were registered as 4D flow images using the volumetric rigid registration method (i.e., elastix) in the 3D Slicer (www.slicer.org) image software package to reserve the velocity information in 4D flow MRI. After image registration, the registered TOF images were utilized to generate the visualized 3D vessel model. In detail, algorithms, including threshold segmentation, connected domain selection, surface extraction, and smoothing, were used to segment and reconstruct the 3D triangular-meshed vessel model in our in-house software. Then, the inward normal vector for each mesh node was calculated for the subsequent hemodynamics computation, which was based on the normal vectors of the adjacent triangular facets using the angle-weighted average method. The postprocessing flowchart is shown in Figure 3. The postprocess was similar to the method of MR fluid dynamics reported and validated in previous studies by Petersson et al. (25) and Isoda et al. (26).
The preprocessing steps of 4D flow MRI included eddy current correction and velocity mask application. After preprocessing and vessel wall surface smoothing, the WSS denoting the frictional force of blood shearing on the vessel wall was calculated with the following formula when considering blood as a Newtonian fluid:
where µ is the dynamic viscosity, v is the velocity parallel to the vessel wall, and x is the vertical distance from the vessel wall. Here, the velocity was estimated from a voxel (1 mm) at the wall and its adjacent voxel in the direction toward the center of the vessel, and the estimation of WSS was conducted based on a validated analysis method using parabolic fitting (25,26). Then, the time-averaged WSS (TAWSS) was calculated based on the obtained WSS within a cardiac cycle, as follows:
WSS oscillates during a cardiac cycle. Its degree of oscillation is described by the OSI, which can be calculated based on the WSS vector and its magnitude, as follows (25):
where wssi represents the instantaneous WSS vectors. Here, the estimation of TAWSS and OSI using the abovementioned method was performed based on interpolated 4D flow MRI velocity data at a spatial resolution of 0.5 mm × 0.5 mm × 0.5 mm.
The hemodynamic parameters of the curved M1 segment of the MCA were analyzed. The WSS parameters, including mean TAWSS (TAWSSmean, average value of all points on the targeted regional vessel), minimum TAWSS (TAWSSmin, minimum value of all points on the targeted regional vessel), maximum TAWSS (TAWSSmax, maximum value of all points on the targeted regional vessel), and OSI parameters (maximum OSI (OSImax) were calculated for the circumferential wall of each location of each vessel. The coefficient of variation of TAWSS (TAWSSCV), which was used to quantify the non-uniformity of the spatial distribution of WSS on the targeted regional vessel, was calculated as follows, where TAWSSstd is the standard deviation of TAWSS on all spatial points and TAWSSmean is the average value of those:
Statistical analysis
The Shapiro-Wilk test was used to check normal distribution. Continuous variables were expressed as mean ± standard deviation for normally distributed data and as median with range for the non-normally distributed data. Categorical variables were expressed as absolute or relative frequencies. Comparisons of the WSS and OSI parameters between the proximal and curved sections, proximal and distal sections, as well as the curved and distal sections of the curved M1 segments were performed by the Kruskal-Wallis H test due to the non-normally distributed data, and all pairwise comparisons were performed using the Kruskal-Wallis one-way analysis of variance (ANOVA; k samples). Comparisons of the WSS and OSI parameters between the inner curvature and outer curvature of the curved M1 section were performed by the independent samples t-test for the normally distributed data and the Mann-Whitney U test for the non-normally distributed data. A P value <0.05 was considered statistically significant. All statistical analyses were performed using the SPSS 24.0 statistical software package (IBM Corp., Armonk, NY, USA).
Results
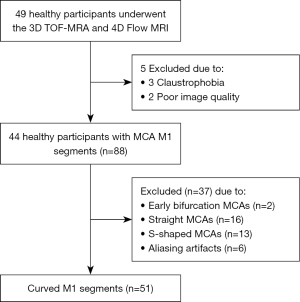
The participant enrollment flow diagram is shown in Figure 4. Of the 49 healthy individuals enrolled in this study, 5 participants were excluded due to claustrophobia for MRI examination (n=3) and scans of poor image quality (n=2). Therefore, 44 healthy participants (18 males; mean age: 27.16±5.69 years; range, 20 to 51 years) with 88 M1 segments were included in this study. On the 3D TOF MRA, no abnormality was found in any participants. We excluded 37 M1 segments due to early bifurcation (defined as that occurring within 1 cm of the MCA origin) (n=2) (27), straight MCAs (n=16), S-shaped MCAs (n=13), and aliasing artifacts (n=6). Finally, 51 curved M1 segments were included in the analysis.
Distribution variation of WSS and OSI at different sections of curved M1 segment
The WSS and OSI parameters at different sections along the long axis of the curved M1 segment are listed in Table 2. A significant difference was found in the TAWSSmin, TAWSSCV, and OSImax among the proximal, curved, and distal sections (all P<0.01). The curved M1 section had significantly lower TAWSSmin values than the proximal and distal sections (P=0.031 and P=0.002, respectively) and the curved M1 section had significantly higher OSImax values than the distal section (P=0.001). Furthermore, the TAWSSCV values were found to be significantly different between the curved and proximal sections (P=0.001), as well as between the curved and distal sections (P<0.001) (Figure 5).
Table 2
| Parameters | Curved M1 segments (n=51) | P value | ||
|---|---|---|---|---|
| Proximal | Curved | Distal | ||
| WSS (Pa) | ||||
| TAWSSmean | 1.39 (1.20–1.72) | 1.33 (1.16–1.59) | 1.36 (1.06–1.56) | 0.708 |
| TAWSSmin | 0.65 (0.46–0.85) | 0.46 (0.34–0.74) | 0.68 (0.48–0.93) | 0.006** |
| TAWSSmax | 2.09 (1.90–2.35) | 2.10 (1.91–2.64) | 2.03 (1.65–2.29) | 0.067 |
| TAWSSCV | 0.22 (0.19–0.30) | 0.32 (0.24–0.36) | 0.21 (0.16–0.27) | <0.001** |
| OSI | ||||
| OSImax | 0.07 (0.02–0.11) | 0.08 (0.03–0.21) | 0.04 (0.01–0.10) | 0.004** |
Values are median (interquartile range). **, indicates a statistical significance (P<0.01). WSS, wall shear stress; OSI, oscillatory shear index; TAWSSmean, mean values of time-averaged WSS; TAWSSmin, minimum values of time-averaged WSS; TAWSSmax, maximum values of time-averaged WSS; TAWSSCV, the coefficient of variation of time-averaged WSS; OSImax, maximum values of the oscillatory shear index; Pa, Pascal.

Regional variation of WSS and OSI at inner and outer curvatures of curved M1 section
The WSS and OSI parameters at the inner and outer curvatures of the curved M1 section are listed in Table 3. At the cross-sectional plane of the curved M1 section, it was found that the TAWSSmean (P=0.002), TAWSSmin (P=0.013) and TAWSSmax values (P=0.015) at the inner curvature were significantly lower than those at the outer curvature (Figure 6) and the OSImax values (P=0.002) at the inner curvature were significantly higher than those at the outer curvature.
Table 3
| Parameters | Curved M1 section | P value | |
|---|---|---|---|
| Outer curvature | Inner curvature | ||
| WSS (Pa) | |||
| TAWSSmean | 1.49±0.37 | 1.26±0.51 | 0.002** |
| TAWSSmin | 0.75 (0.51–0.91) | 0.51 (0.34–0.84) | 0.013* |
| TAWSSmax | 2.13±0.44 | 1.91±0.57 | 0.015* |
| OSI | |||
| OSImax | 0.05 (0.02–0.07) | 0.08 (0.04–0.17) | 0.002** |
Values were expressed as mean ± standard deviation or median (interquartile range). *, indicates a statistical significance (P<0.05); **, indicates a statistical significance (P<0.01). WSS, wall shear stress; OSI, oscillatory shear index; TAWSSmean, mean values of time-averaged WSS; TAWSSmin, minimum values of time-averaged WSS; TAWSSmax, maximum values of time-averaged WSS; OSImax, maximum values of the oscillatory shear index; Pa, Pascal.
Discussion
In the current study, we reported the WSS and OSI parameters of curved M1 segments in healthy participants using 4D flow MRI. There were significant distribution and regional variation of the WSS and OSI parameters among the different sections of the curved M1 segments, including the inner and outer curvatures of the curved M1 section.
Our results showed that the WSS and OSI values distributed along the long axis of the curved MCA were not uniform. In the curved M1 segment, the curved M1 section was found to have lower TAWSSmin values than the proximal and distal sections and the curved M1 section was found to have higher OSImax values than the distal section. Since atherosclerotic plaque development is associated with regions exposed to low WSS and high OSI, our results might suggest that the curved M1 sections have hemodynamic features more conducive to atherosclerotic disease. The TAWSSCV is another interesting index used in our study to reflect the varying degree of TAWSS values among different locations along the circumferential wall. In our study, the curved M1 section demonstrated the highest TAWSSCV, significantly higher than both the proximal and distal sections. This morphological change may lead to a big difference in the WSS of the curvature region. The TAWSSCV was more sensitive in detecting unevenly distributed WSS values around the circumferential wall than other parameters.
In the current study, the inner curvature was found to have higher OSI and lower WSS parameters than the outer curvature of the curved M1 section. This certain shear force feature at the inner curvature of the curved vessel has also been demonstrated in many other vessels. Previous studies have reported that a vessel with geometric curvature demonstrates the obvious centrifugal flow pattern, with blood flow skewed to the outer curvature and reduced WSS at the inner curvature (28,29). The specific distribution feature of WSS and OSI at the curvature of vessels is probably related to the formation of vascular diseases. A flow-sensitive 4D MRI study on the aorta demonstrated that low WSS and a high OSI are distributed at the inner curvature and supra-aortic branch, which closely resembles the typical locations of atherosclerotic lesions (30). The predilection for plaque to be located at the inner curvature, both in U-shaped and inverted U-shaped MCAs (14) as well as the tortuous basilar artery, has also been defined by investigators (31). The results of the current study might indicate possible underlying hemodynamic mechanisms for the formation and development of atherosclerotic cerebrovascular diseases.
In this study, 4D flow MRI and TOF MRA images were integrated for the calculation and visualization of MCA hemodynamics. 4D flow imaging allows for direct in vivo measurement of 3D blood velocity, which can be utilized for the evaluation of hemodynamics, including WSS and the OSI (32,33). It could be considered as an in vivo individual assessment method for predicting the preferential locations of AS plaques or cerebral aneurysms. Furthermore, the TOF MRA images were used to segment and locate the boundary of a vessel as a supplement to the 4D flow MRI, due to the better signal contrast of blood flow in the TOF MRA images which improved the accuracy of vessel segmentation. The method used in the current study can also be applied in future studies to the hemodynamic assessment of intracranial arteries in other vascular diseases.
The 4D flow MRI has been gradually applied to the measurement of cerebrovascular hemodynamics, including intracranial atherosclerotic disease, intracranial aneurysms, and AVMs. Intracranial atherosclerotic plaques can alter local and global hemodynamics. Conversely, local hemodynamic status such as WSS may be related to AS plaque distribution and irregular plaque surface morphology (1,34). In a study of unruptured cerebral aneurysms, it was found that the average WSS and maximum blood flow correlated with the size of aneurysms (2). One hemodynamic study of AVMs showed that the WSS plays a vital role in vascular remodeling to monitor AVM response to treatment or understand other high-flow vascular pathologies (35). In recent years, the developments of highly accelerated 4D flow MRI (36) and multiple velocity encoding (multi-venc) (37) 4D flow MRI have resulted in increased flexibility of its application, which could be extended to the study of cerebrovascular diseases.
Limitations
There were several limitations of the current study. First, the spatial resolution of the 4D flow sequence was set according to the recommendation (38). Approximately 3 voxels were acquired across the M1 segment using the spatial resolution of 1.0 mm × 1.0 mm × 1.0 mm. The number of voxels across the vessel of interest will increase with higher spatial resolution, which will help to improve the accuracy of the WSS calculation. Therefore, in this study, the interpolated 4D flow MRI data with a spatial resolution of 0.5 mm × 0.5 mm × 0.5 mm were used to improve the hemodynamic evaluation. Also, as Ha et al. (39) have mentioned, accurate segmentation of the geometrical boundary of the vessel is essential for assessing the flow parameters on 4D flow MRI. In this study, the TOF MRA images were used for vessel segmentation. Although we think a higher contrast-to-noise ratio (CNR) might improve the accuracy of velocity calculations, the discrepancies between 4D flow MRI and TOF MRA-derived segmentation might be a very interesting topic for future study. Combining CFD models provides future direction for increasing the spatial resolution and further increasing the WSS calculation accuracy based on the boundary condition of velocity measured by 4D flow MRI. Second, the sample size included in this study may not reflect the WSS distribution characteristics in a large population. The tortuosity of MCAs is more obvious in older patients (40). Given the relatively young age of our study participants, the results might have been affected by age bias. Furthermore, there may have been some potential operator bias in the measurements of quantitative metrics. In a future study, a quantitative method would be needed to verify the result in a group of participants of a larger sample size. Moreover, the WSS were presented as time-averaged values in this study. Although the OSI was used to represent the temporal changes of WSS, the WSS distribution features at systolic, diastolic, or other phases of the cardiac cycle may provide more detailed information, which could help to better understand the hemodynamic mechanisms. Finally, only normal MCAs were studied. The investigation of the hemodynamics of stenosed MCAs would provide more information about AS-related hemodynamic features.
Conclusions
According to our findings, there are distribution variation in the WSS and OSI parameters at the curved M1 section of curved MCAs, and the inner curvature of the curved M1 section has the lowest WSS and highest OSI distribution. The local hemodynamic features of the curved MCA may be related to the predilection for atherosclerotic plaque development.
Acknowledgments
The authors thank Dr. An’xin Wang for the statistical advice of this study.
Funding: This work was supported by Beijing Municipal Natural Science Foundation (Nos. 7212028 and 7162056); Beijing Municipal Health System High Level Medical Personnel Discipline Backbone Project (No. 2015-3-037).
Footnote
Reporting Checklist: The authors have completed the STROBE reporting checklist. Available at https://qims.amegroups.com/article/view/10.21037/qims-22-67/rc
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://qims.amegroups.com/article/view/10.21037/qims-22-67/coif). The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013) and supported by the Institutional Review Board of Beijing Tiantan Hospital, Capital Medical University (No. KY 2019-053-02). Written informed consent was provided by all study participants.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Wu C, Schnell S, Vakil P, Honarmand AR, Ansari SA, Carr J, Markl M, Prabhakaran S. In Vivo Assessment of the Impact of Regional Intracranial Atherosclerotic Lesions on Brain Arterial 3D Hemodynamics. AJNR Am J Neuroradiol 2017;38:515-22. [Crossref] [PubMed]
- Zhang M, Peng F, Li Y, He L, Liu A, Li R. Associations between morphology and hemodynamics of intracranial aneurysms based on 4D flow and black-blood magnetic resonance imaging. Quant Imaging Med Surg 2021;11:597-607. [Crossref] [PubMed]
- Chen X, Cooke DL, Saloner D, Nelson J, Su H, Lawton MT, Hess C, Tihan T, Zhao Y, Kim H. Higher Flow Is Present in Unruptured Arteriovenous Malformations With Silent Intralesional Microhemorrhages. Stroke 2017;48:2881-4. [Crossref] [PubMed]
- Roux E, Bougaran P, Dufourcq P, Couffinhal T. Fluid Shear Stress Sensing by the Endothelial Layer. Front Physiol 2020;11:861. [Crossref] [PubMed]
- Shakur SF, Amin-Hanjani S, Mostafa H, Charbel FT, Alaraj A. Hemodynamic Characteristics of Cerebral Arteriovenous Malformation Feeder Vessels With and Without Aneurysms. Stroke 2015;46:1997-9. [Crossref] [PubMed]
- Lv N, Karmonik C, Chen S, Wang X, Fang Y, Huang Q, Liu J. Wall Enhancement, Hemodynamics, and Morphology in Unruptured Intracranial Aneurysms with High Rupture Risk. Transl Stroke Res 2020;11:882-9. [Crossref] [PubMed]
- Teng Z, Wang S, Tokgoz A, Taviani V, Bird J, Sadat U, Huang Y, Patterson AJ, Figg N, Graves MJ, Gillard JH. Study on the association of wall shear stress and vessel structural stress with atherosclerosis: An experimental animal study. Atherosclerosis 2021;320:38-46. [Crossref] [PubMed]
- Strecker C, Krafft AJ, Kaufhold L, Hüllebrandt M, Treppner M, Ludwig U, Köber G, Hennemuth A, Hennig J, Harloff A. Carotid Geometry and Wall Shear Stress Independently Predict Increased Wall Thickness-A Longitudinal 3D MRI Study in High-Risk Patients. Front Cardiovasc Med 2021;8:723860. [Crossref] [PubMed]
- Markl M, Brendecke SM, Simon J, Barker AJ, Weiller C, Harloff A. Co-registration of the distribution of wall shear stress and 140 complex plaques of the aorta. Magn Reson Imaging 2013;31:1156-62. [Crossref] [PubMed]
- Morbiducci U, Kok AM, Kwak BR, Stone PH, Steinman DA, Wentzel JJ. Atherosclerosis at arterial bifurcations: evidence for the role of haemodynamics and geometry. Thromb Haemost 2016;115:484-92. [Crossref] [PubMed]
- Doutel E, Viriato N, Carneiro J, Campos JBLM, Miranda JM. Geometrical effects in the hemodynamics of stenotic and non-stenotic left coronary arteries-numerical and in vitro approaches. Int J Numer Method Biomed Eng 2019;35:e3207. [Crossref] [PubMed]
- Spanos K, Petrocheilou G, Karathanos C, Labropoulos N, Mikhailidis D, Giannoukas A. Carotid Bifurcation Geometry and Atherosclerosis. Angiology 2017;68:757-64. [Crossref] [PubMed]
- Denswil NP, van der Wal AC, Ritz K, de Boer OJ, Aronica E, Troost D, Daemen MJAP. Atherosclerosis in the circle of Willis: Spatial differences in composition and in distribution of plaques. Atherosclerosis 2016;251:78-84. [Crossref] [PubMed]
- Kim BJ, Yoon Y, Lee DH, Kang DW, Kwon SU, Kim JS. The shape of middle cerebral artery and plaque location: high-resolution MRI finding. Int J Stroke 2015;10:856-60. [Crossref] [PubMed]
- Yu YN, Li ML, Xu YY, Meng Y, Trieu H, Villablanca JP, Gao S, Feng F, Liebeskind DS, Xu WH. Middle cerebral artery geometric features are associated with plaque distribution and stroke. Neurology 2018;91:e1760-9. [Crossref] [PubMed]
- Razavi SE, Farhangmehr V, Zendeali N. Numerical investigation of the blood flow through the middle cerebral artery. Bioimpacts 2018;8:195-200. [Crossref] [PubMed]
- Stankovic Z, Allen BD, Garcia J, Jarvis KB, Markl M. 4D flow imaging with MRI. Cardiovasc Diagn Ther 2014;4:173-92. [PubMed]
- Jacobs K, Rigdon J, Chan F, Cheng JY, Alley MT, Vasanawala S, Maskatia SA. Direct measurement of atrioventricular valve regurgitant jets using 4D flow cardiovascular magnetic resonance is accurate and reliable for children with congenital heart disease: a retrospective cohort study. J Cardiovasc Magn Reson 2020;22:33. [Crossref] [PubMed]
- Guala A, Teixido-Tura G, Dux-Santoy L, Granato C, Ruiz-Muñoz A, Valente F, Galian-Gay L, Gutiérrez L, González-Alujas T, Johnson KM, Wieben O, Sao Avilés A, Evangelista A, Rodriguez-Palomares J. Decreased rotational flow and circumferential wall shear stress as early markers of descending aorta dilation in Marfan syndrome: a 4D flow CMR study. J Cardiovasc Magn Reson 2019;21:63. [Crossref] [PubMed]
- Orita E, Murai Y, Sekine T, Takagi R, Amano Y, Ando T, Iwata K, Obara M, Kumita S. Four-Dimensional Flow MRI Analysis of Cerebral Blood Flow Before and After High-Flow Extracranial-Intracranial Bypass Surgery With Internal Carotid Artery Ligation. Neurosurgery 2019;85:58-64. [PubMed]
- Wen B, Tian S, Cheng J, Li Y, Zhang H, Xue K, Zhang Z, Fan Y, Wu B. Test-retest multisite reproducibility of neurovascular 4D flow MRI. J Magn Reson Imaging 2019;49:1543-52. [Crossref] [PubMed]
- Juffermans JF, Westenberg JJM, van den Boogaard PJ, Roest AAW, van Assen HC, van der Palen RLF, Lamb HJ. Reproducibility of Aorta Segmentation on 4D Flow MRI in Healthy Volunteers. J Magn Reson Imaging 2021;53:1268-79. [Crossref] [PubMed]
- Han J, Qiao H, Li X, Li X, He Q, Wang Y, Cheng Z. The three-dimensional shape analysis of the M1 segment of the middle cerebral artery using MRA at 3T. Neuroradiology 2014;56:995-1005. [Crossref] [PubMed]
- Kim BJ, Kim SM, Kang DW, Kwon SU, Suh DC, Kim JS. Vascular tortuosity may be related to intracranial artery atherosclerosis. Int J Stroke 2015;10:1081-6. [Crossref] [PubMed]
- Petersson S, Dyverfeldt P, Ebbers T. Assessment of the accuracy of MRI wall shear stress estimation using numerical simulations. J Magn Reson Imaging 2012;36:128-38. [Crossref] [PubMed]
- Isoda H, Ohkura Y, Kosugi T, Hirano M, Alley MT, Bammer R, Pelc NJ, Namba H, Sakahara H. Comparison of hemodynamics of intracranial aneurysms between MR fluid dynamics using 3D cine phase-contrast MRI and MR-based computational fluid dynamics. Neuroradiology 2010;52:913-20. [Crossref] [PubMed]
- Oo EM, Saw KEE, Oo HN, Than T, Thida K. Variable Anatomy of the Middle Cerebral Artery from Its Origin to the Edge of the Sylvian Fissure: A Direct Fresh Brain Study. ScientificWorldJournal 2021;2021:6652676. [Crossref] [PubMed]
- Takeuchi S, Karino T. Flow patterns and distributions of fluid velocity and wall shear stress in the human internal carotid and middle cerebral arteries. World Neurosurg 2010;73:174-85; discussion e27. [Crossref] [PubMed]
- Malik J, Novakova L, Valerianova A, Chytilova E, Lejsek V, Buryskova Salajova K, Lambert L, Grus T, Porizka M, Michalek P. Wall Shear Stress Alteration: a Local Risk Factor of Atherosclerosis. Curr Atheroscler Rep 2022;24:143-51. [Crossref] [PubMed]
- Frydrychowicz A, Stalder AF, Russe MF, Bock J, Bauer S, Harloff A, Berger A, Langer M, Hennig J, Markl M. Three-dimensional analysis of segmental wall shear stress in the aorta by flow-sensitive four-dimensional-MRI. J Magn Reson Imaging 2009;30:77-84. [Crossref] [PubMed]
- Zhou L, Yan Y, Du H, Ni X, Wang G, Wang Q. Plaque features and vascular geometry in basilar artery atherosclerosis. Medicine (Baltimore) 2020;99:e19742. [Crossref] [PubMed]
- Soulat G, McCarthy P, Markl M. 4D Flow with MRI. Annu Rev Biomed Eng 2020;22:103-26. [Crossref] [PubMed]
- Morgan AG, Thrippleton MJ, Wardlaw JM, Marshall I. 4D flow MRI for non-invasive measurement of blood flow in the brain: A systematic review. J Cereb Blood Flow Metab 2021;41:206-18. [Crossref] [PubMed]
- Leng X, Lan L, Ip HL, Abrigo J, Scalzo F, Liu H, et al. Hemodynamics and stroke risk in intracranial atherosclerotic disease. Ann Neurol 2019;85:752-64. [Crossref] [PubMed]
- Alaraj A, Shakur SF, Amin-Hanjani S, Mostafa H, Khan S, Aletich VA, Charbel FT. Changes in wall shear stress of cerebral arteriovenous malformation feeder arteries after embolization and surgery. Stroke 2015;46:1216-20. [Crossref] [PubMed]
- Peper ES, Gottwald LM, Zhang Q, Coolen BF, van Ooij P, Nederveen AJ, Strijkers GJ. Highly accelerated 4D flow cardiovascular magnetic resonance using a pseudo-spiral Cartesian acquisition and compressed sensing reconstruction for carotid flow and wall shear stress. J Cardiovasc Magn Reson 2020;22:7. [Crossref] [PubMed]
- Schnell S, Ansari SA, Wu C, Garcia J, Murphy IG, Rahman OA, Rahsepar AA, Aristova M, Collins JD, Carr JC, Markl M. Accelerated dual-venc 4D flow MRI for neurovascular applications. J Magn Reson Imaging 2017;46:102-14. [Crossref] [PubMed]
- Markl M, Frydrychowicz A, Kozerke S, Hope M, Wieben O. 4D flow MRI. J Magn Reson Imaging 2012;36:1015-36. [Crossref] [PubMed]
- Ha H, Kim GB, Kweon J, Lee SJ, Kim YH, Lee DH, Yang DH, Kim N. Hemodynamic Measurement Using Four-Dimensional Phase-Contrast MRI: Quantification of Hemodynamic Parameters and Clinical Applications. Korean J Radiol 2016;17:445-62. [Crossref] [PubMed]
- Kim BJ, Lee KM, Lee SH, Kim HG, Kim EJ, Heo SH, Chang DI, Kim JS. Ethnic Differences in Intracranial Artery Tortuosity: A Possible Reason for Different Locations of Cerebral Atherosclerosis. J Stroke 2018;20:140-1. [Crossref] [PubMed]


