
Application of a Markov chain Monte Carlo method for robust quantification in chemical exchange saturation transfer magnetic resonance imaging
Introduction
Chemical exchange saturation transfer (CEST) magnetic resonance imaging (MRI) is a promising imaging modality (1-3). It allows for indirect solute molecule detection and reflection of the chemical environment of tissue, such as pH and temperature, through selectively saturating labile protons and measuring water signal changes (4,5). By measuring the reduction in the water signal, it is possible to quantitatively analyze the effect of CEST. By virtue of these properties, various endogenous metabolites and exogenous agents have been used in research to detect diseases (6,7). For example, one of the most commonly used endogenous CEST effects in amide proton transfer (APT) imaging is high pH sensitivity due to the dependence on the exchange rate of amide groups. This characteristic has been applied to diagnose tumors and acute stroke (8-13).
Despite the many advantages of CEST MRI, its mechanism is complex, and it is challenging to accurately quantify the CEST effects of interest. Current analysis methods mainly rely on Z-spectra (the water signal as a function of resonance frequency offsets) (14), such as magnetization transfer ratio asymmetry (MTRasym) (15), the three-offsets method (16), Lorentzian line shape-based fitting (17), Omega plots (18), and the quantification of exchange rate using varying saturation power/time methods, to estimate the exchange rate (19,20). However, limitations exist with these approaches. In the case of MTRasym, the water proton signal obtained upon saturation at a single offset frequency (Ssat) is compared to the water signal without saturation (S0). Although this approach is relatively simple to implement, MTRasym can be contaminated by the upfield nuclear Overhauser enhancement (NOE) signals of mobile and semi-solid macromolecules due to the bias induced by these non-symmetric effects. Lorentzian fitting methods introduce a Lorentzian line shape model for the proton transfer rate and direct water saturation quantification, which results in the separation of CEST effects from competing effects, such as spillover (21) and magnetization transfer (MT) (22). However, the model is fitted using least squares; consequently, targets suffer from typical instabilities caused by a low signal-to-noise ratio and dependence on initial and boundary values (23). Furthermore, despite being able to determine the interesting parameter exchange rate, the Omega plot, quantifying exchange using saturation time (QUEST) and quantifying exchange using saturation power (QUESP) methods require scans with varying saturation pulse power, which results in a long scanning time.
In contrast to these conventional quantification methods, Bloch equations coupled with exchange terms [Bloch-McConnell (BM) equations] can numerically simulate chemical exchange to quantify CEST contrast (24,25). BM equations modified for chemical exchange give exquisite delineation for bulk water and multiple labile proton pools, whose magnetic resonance behavior can be fully described (26). However, an obstacle for the model is the complexity of fitting a large number of unknown parameters, including the concentration of CEST agents or amide protons, exchange and relaxation properties, and parameters that vary with experimental conditions, such as magnetic field strength and radiofrequency (RF) power (27). Moreover, BM equations are not easily scalable, and it is tedious to apply them to describe multi-pool CEST contrast beyond three labile proton groups (28). These challenges make it difficult to accurately quantify CEST effects; therefore, many previous quantitative methods opt for simplified models over BM equations.
In the present study, we aimed to investigate an approach of probabilistic model-based analysis to estimate the saturation parameter and quantify the CEST effect. The Bayesian inference model provides a framework that combines prior knowledge and measured data, reducing the risk of over-fitting (29). Nevertheless, the posterior distribution for the BM equation model is still complex. To facilitate the calculation process, we applied a Markov chain Monte Carlo (MCMC) method (30), which has been shown to be applicable to the problem of solving complex models (31).
The MCMC quantification method adopted in this study included two parts. First, the prior, likelihood, and posterior distributions based on Bayesian inference theory were constructed. Second, we generated a Markov chain and used the Metropolis-Hastings (MH) algorithm for the sampling process until the Markov chain converged (32).
Both simulated experiments and in vivo experiments in ischemic stroke rats were conducted. To assess the performance of the MCMC-based CEST quantification method, we chose the Lorentzian line-shape fitting method and the quantification method as the benchmark methods for the simulation and animal studies, respectively.
Methods
Bayesian inference framework
The fitting model was based on Bayesian inference theory. According to this theory, if there is a set of unseen parameters Θ={θ1,…θi,…θn}, including n parameters, whose posterior distribution p(Θ|S) is equal to the prior distribution p(Θ) multiplied by the likelihood distribution p(S|Θ), the posterior expectation can be calculated using the equation below to acquire the closest estimate to the true values of parameters:
where p(Θ) is equal to , whose means and precisions are shown in Table 1. The posterior probability and the likelihood p(S|Θ) are assumed to be a product of a series of Gaussian distributions, which can be expressed by the probability density function, as follows:
Table 1
| Parameter | Water | Amide (3.5 ppm) | Amine (2 ppm) | NOE (–3.5 ppm) | MT (–2.3 ppm) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | SD | Mean | SD | Mean | SD | Mean | SD | Mean | SD | |||||
| T1 (s) | 3.3 | 0.01 | – | – | – | – | – | – | – | – | ||||
| T2 (ms) | 0.05 | 0.001 | 0.05 | 0.001 | 0.05 | 0.001 | 2 | 0.01 | 40 | 0.2 | ||||
| Ksw (Hz) | – | – | 20 | 0.1 | 150 | 0.5 | 25 | 0.1 | 25 | 0.1 | ||||
| fs | – | – | 0.001 | 10−5 | 0.001 | 10−5 | 0.001 | 10−5 | 0.1/0.01/0.001 | 10−4 | ||||
NOE, nuclear Overhauser enhancement; MT, magnetization transfer.
In the context of CEST, S={S1,…,Si,…,Sn} represents the measured Z-spectrum data and Θ corresponds to the set of parameters to be estimated, such as the exchange and relaxation rates, based on the given BM model f(Θ).
In this study, we transformed the probabilities into logarithmic form for model linearization and to simplify the calculation process (33).
Markov chain Monte Carlo
As described above, the Bayesian inference approach can estimate the unseen parameters of BM equations. To do so, the marginal likelihood distribution of each parameter must be solved. However, it is often difficult to obtain an analytical solution or generate a large number of integral operations. Sometimes, even an explicit evaluation of the integrals is not possible. Therefore, numerical approximation techniques may be used to make up for these deficiencies. The MCMC method is such an alternative approach whereby samples are taken from distributions directly and sample estimates of the quantities of interest are obtained; thereby, the complex calculations are implicitly performed. The MCMC approach first constructs an aperiodic and irreducible Markov chain. Then, if the chain is run for long enough, the probability distribution of the Markov chain’s state will converge consequentially. When the Markov chain reaches a steady state, the simulated samples will depict the required distribution. In this study, the MH algorithm, which samples each parameter θi from its respective posterior distribution, was chosen as a sampling method.
The MCMC process involved the following steps: (I) initial values were generated for each parameter by randomly sampling from the uniform distribution in a range of 0 to 1, and the number of iterations (N) was set; (II) the new sample parameter values were updated as a proposal and this proposal was accepted or rejected according to the log-probability of the posterior probability; and (III) after the iteration process, the Markov chain eventually reached a stable stage, and the sampling of each parameter could be regarded as the actual estimated value. The process flow chart is shown in Figure 1.
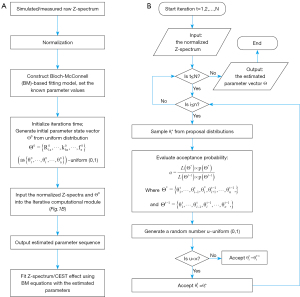
BM equations
The analytical solution of BM equations described by Zaiss et al. (34) was adopted as the simulation and fitting models in this study. Water z-magnetization after irradiation at the RF frequency offset Δω, normalized by the equilibrium magnetization [Z(Δω)=Ssat(Δω)/S0] was calculated using the following equation:
where θ represents the flip angle, R1a is the longitudinal relaxation rate of the water pool, and R1ρ is the longitudinal relaxation rate in the rotating frame, in the case that the MT pool exists, which could be described by:
where Reff is the longitudinal relaxation rate of the water pool, which is the origin of the spillover effect. In the following equation, R2a is the transverse relaxation rate of the water pool:
and is the exchange-dependent relaxation, which combines the distribution of all the exchange pools. A single was approximated according to the following equation:
where kba is the exchange rate of pool b to water, fb is the solute concentration, Δωb is the frequency offset in respect to the CEST pool b, and a is the labeling efficiency, which was approximated as follows:
Since is a Lorentzian function of Δωb, the linewidth was calculated as:
where ω1=B1γ =267.5 rad · S−1 (in which γ and B1 are the gyromagnetic ratio and RF power, respectively) and represents the nutation rate.
For MT (pool e), the relaxation was calculated as follows:
where , , and .
Simulation study
Z-spectra were simulated in the Matlab platform (The MathWorks, Inc., Natick, MA, USA) using the general solution of the above-mentioned BM equations. The simulation parameters that were estimated are shown in Table 2. The spectra were sampled at saturation frequency offsets Δωa from –5 to 5 ppm in steps of 0.1 ppm. The parameter values of the pulse sequence and the MRI scanner were as follows: gyromagnetic ratio γ=267.5 Mrad/T and B0=7 T. Multiple Z-spectra with varying levels of RF irradiation power were simulated to assess the robustness of our method with the values of B1=0.5, 1, 2 µT.
Table 2
| Pool case | Parameter | Water | Amide (3.5 ppm) | Amine (2 ppm) | NOE (–3.5 ppm) | MT (–2.3 ppm) |
|---|---|---|---|---|---|---|
| 2-pool | T1 (s) | 2.2 | – | – | – | |
| T2 (ms) | 36 | 36 | – | – | – | |
| Ksw (Hz) | – | 10 | – | – | – | |
| fs | 1 | 0.004 | – | – | – | |
| 5-pool | T1 (s) | 2.2 | – | – | – | 2.2 |
| T2 (ms) | 36 | 36 | 36 | 0.4 | 0.02 | |
| Ksw (Hz) | – | 10 | 100 | 20 | 20 | |
| fs | 1 | 0.004 | 0.002 | 0.0033 | 0.4/0.04/0.004 |
BM, Bloch-McConnell; T1, longitudinal relaxation time; T2, transverse relaxation time; Ksw, solute-water exchange rate; fs, solute concentration.
A 2-pool model was assumed to represent a typical case of APT phantoms, with one pool describing the water protons (pool a) and the other pool describing the amide protons (pool b). Also, a 5-pool model was generated to mimic the complex in vivo biological environment. Pools a, b, c, d, and e represented water, amide, amine, NOE, and MT, respectively.
Acquisition of CEST data
Data acquisition was performed on a 7 Tesla horizontal bore scanner (Bruker Biospec, Germany) using a transmit-receiver volume coil (diameter =40 mm). After the acquisition of T2-weighted images for multiple slices, CEST MRI was acquired at a coronal slice at the center of the striatum using a continuous wave presaturation pulse (Tsat=2,500 ms) followed by a rapid acquisition with relaxation enhancement (RARE) readout (RARE factor =32; TR/TE =5,000 ms/4 ms). For a single CEST scan, 50 Z-spectra images with saturation offsets (Δω) at increments from –10 to 10 ppm were collected at B1-sat of 1 µT (acquisition time =255 s). The B0 inhomogeneity map was then obtained using a water saturation shift referencing method (35), in which the saturation images with a weak saturation pulse (B1–sat =0.5 µT; Tsat=500 ms) were swept from –1 to 1 ppm (0.1 ppm per step). The S0 image without the saturation pulse was collected for signal normalization. Diffusion-weighted imaging (DWI) was conducted using a pulsed-gradient spin-echo sequence with b value =2,000 s/mm2 (36,37). The other parameters were as follows: slice thickness =1 mm, FOV =34×28 mm2, and matrix size =94×64.
Animal model
The animal study was approved by the ethics board of Weifang Medical University and was conducted in compliance with institutional guidelines for the care and use of animals. Adult male Sprague Dawley rats (weight, 240 to 270 g) underwent middle cerebral artery occlusion via an intraluminal suture (38). Two hours after the occlusion, the nylon suture was withdrawn for reperfusion. During the surgical procedure, the core temperature of the r was maintained at 37±0.5 ℃, and their respiratory rates were monitored online. All rats were immobilized and anesthetized with a 2–98% isoflurane-oxygen mixture during data acquisition.
Data analysis
During the MCMC process, there were two considerations depending on the known parameters.
When there were too many unknown parameters to obtain a unique solution, the predicted parameters were one of the solution sets that satisfied the BM equation but could not reflect the real physical properties of the parameters. These parameters could be used for CEST quantification based on the BM model. Five unknown parameters (R1a, R2a, R2b, Rba, fb) (for the 2-pool model) or 15 unknown parameters (R1a, R2a, R2b, Rba, fb, R2c, Kca, fc, R2d, Kda, fd, R1e, R2e, Kea, fe) (for the 5-pool model) needed to be estimated.
After the elimination of some unknown parameters, for example by using other methods to correct water and MT effects or by measuring the concentration of some solutes, we could obtain unique solutions. In this case, six unknown parameters (R1b, Kba, R2c, Kca, R2d, Kda) (for the 5-pool model) needed to be estimated.
For the simulated data, we used the estimated parameters to fit Z-spectra and CEST effect spectra, including and . These metrics could be respectively described using analytical BM equations as follows:
The in Eq. [10] represents the MT and spillover-corrected quantification (39) and a mixture of various CEST effects, which could be quantified by the MCMC and conventional Lorentzian line shape-based methods. Using the conventional method, the Zlab represents the measured Z-spectrum, and the Zref is determined using a 2-pool (water and semi-solid MT) least-square fitting for the Z-spectrum.
The in Eq. [12] is the quantitative description for an individual CEST effect, such as amide, amine, or NOE.
The fitting qualities were evaluated using the sum of squares error (SSE), the root mean square error (RMSE), and the coefficient of determination (R-square).
For the in vivo data, water saturation shift referencing was performed for the raw Z-spectra data to correct B0 inhomogeneity first, and then the corrected Z-spectra were calculated from the saturated image Ssat and unsaturated reference image S0 as:
The corrected Z-spectra were used as the measured signals.
For the in vivo experiments, the fitting approaches used were the same as those used for the simulated data, and all fits were performed pixel by pixel. Other conventional quantitative approaches, namely the MTRasym and three-offsets, were performed as contrast methods, as follows:
To compare the performance of the methods, we calculated the contrast-to-noise ratios (CNR) between regions of interest (ROIs) using the following equation (40):
where SIS,CO are the mean values of ischemic and contralateral ROIs, respectively, and σCO represents the standard deviation of the contralateral ROI.
The coefficient of variation (CoV) of the whole brain was also calculated, as follows:
where σ and µ are the standard deviation and mean value of the whole brain, respectively.
Results
Simulated experiments
An example of the simulated Z-spectra, together with the fitting results of the MCMC and the residuals between them, is shown in Figure 2. Figure 2A shows the individual Z-spectra simulated for the 2-pool BM model (water pool a and amide pool b), and Figure 2B shows the Z-spectra simulated for the 5-pool model with B1 values equal to 0.5, 1, and 2 µT, respectively. For the 5-pool simulations, different MT concentrations were considered, including the cases equal to 0.4 (red circles), 0.04 (purple circles), and 0.004 (blue circles). All of these simulated Z-spectra were well described by the MCMC fitted spectra, as confirmed in the minimal standard deviation of the fit residuals for the 2-pool case (σres=0.00038) and for the 5-pool case (σres=0.000964).
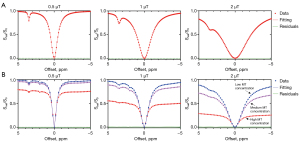
Also, the SSE, RMSE and R-squared metrics were calculated for all cases, and the quantitative results are shown in Table 3. The SSE and RMSE values of the fits were smaller than 10–3, while the R-squared values were close to 1, which indicated the validity of the fitting model.
Table 3
| No. of pools | B1 power (μT) | SSE | RMSE | R-squared |
|---|---|---|---|---|
| 2 | 0.5 | 5.48×10−7 | 7.37×10−5 | 0.9999 |
| 2 | 1 | 4.34×10−5 | 0.00066 | 0.9999 |
| 2 | 2 | 7.61×10−7 | 8.68×10−5 | 0.9999 |
| 5 | 0.5 | 2.74×10−4 | 0.00095 | 0.9999 |
| 5 | 1 | 3.01×10−4 | 0.000997 | 0.9999 |
| 5 | 2 | 2.71×10−4 | 0.000945 | 0.9999 |
MCMC, Markov chain Monte Carlo; SSE, sum of squares error; RMSE, root mean square error.
We also performed the Lorentzian line-shape fitting on these simulated Z-spectra and compared the results with those of the MCMC method. The results are shown in Figure S1.
Figure 3 displays the downfield and spectra simulations of the 5-pool models shown in Figure 2, as well as the corresponding fitted spectra, with B1 values equal to 0.5, 1 and 2 µT, respectively. The fittings (Figure 3A) were obtained using both the MCMC (blue lines) and Lorentzian methods (green lines). The MCMC approach provided good fitting results, while the Lorentzian method had lower fitting accuracy, which was especially obvious at high B1 powers. From individual spectra (Figure 3B), through the calculations using MCMC predicted parameters, the amine (2 ppm) and amide (3.5 ppm) peaks were well separated and fitted, respectively. The modeled spectra described the simulated data reasonably well, with the negligible residuals between the ground truth and fitting results.

A further simulation was performed to assess the capacity of the MCMC method to predict parameters accurately. On the basis of the 5-pool case mentioned above, more saturated information was given, including known exchangeable proton concentrations and MT/spillover effect correction. For each of the nine simulated cases (different B1 powers and MT concentrations) of the 5-pool model, the independent repeat estimation process was performed ten times and the estimated parameters were recorded. Then, the means and standard deviations of these parameters were statistically calculated and visualized (Figure 4, with the values shown in Table 4). The exchange rate estimations are shown in Figure 4A, in which pools b, c, and d represent amide, amine, and NOE, respectively. Figure 4B displays the estimated transverse relaxation rates of these exchanged pools. None of the estimations showed any significant observable biases in respect to the ground truth, and the error between the true and estimated values was less than 0.5% for all parameters.
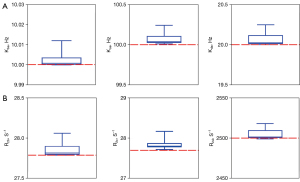
Table 4
| Parameters | Truth | Estimations | Error |
|---|---|---|---|
| Kba (Hz) | 10 | 10.00237 (0.0037) | 0.0237% |
| R2b (ms−1) | 27.78 | 27.85385 (0.088) | 0.2658% |
| Kca (Hz) | 100 | 100.0679 (0.071) | 0.0679% |
| R2c (ms−1) | 27.78 | 27.83646 (0.1276) | 0.203% |
| Kda (Hz) | 20 | 20.064 (0.078) | 0.32% |
| R2d (ms−1) | 2,500 | 2,504.475 (6.384) | 0.179% |
Considering that data is often disturbed by noise in real-world situations, we also assessed the performance of the MCMC method with different signal-to-noise ratios. Gaussian noise of different amplitudes was added to the simulated data, and then the MCMC approach was used to perform curve fittings and parameter estimations. The results are displayed in Figure S2.
Animal experiments
The performance of the MCMC method was also tested in vivo in rats at the early stage of ischemic stroke. The contrast maps at 2 hours after reperfusion are displayed in Figure 5. The T2w, DWI, and raw CEST maps showed relatively little change immediately following ischemia, but the map showed obvious hyperintensity in the ipsilateral ischemic brain, which indicated acidosis. These results show that CEST MRI can be used to detect the pH environment and demonstrate the significance of the quantification method.

Based on the data detailed in Figure 5, two ROIs on the striatum were selected for spectra analysis. The first ROI represented ischemic tissue (hypointense) and the second ROI represented contralateral normal tissue (hyperintense). The spectra analysis results are shown in Figure 6. For the in vivo Z-spectra, the MCMC method also obtained good fitting results. In this period of ischemic stroke, there was less difference in the Z-spectra between these ROIs, while the other spectra showed obvious contrast. Of note, the spectra mixed the effects, which saw the amide peaks become indistinct, whereas the three spectra displayed the effects more intuitively. Of the spectra, the spectra showed the most obvious differences between the ROIs. These results indicated that quantification using the MCMC method may have more advantages than quantification for the analysis of specific CEST effects. The results also suggest that all three CEST effects are potential biomarkers for ischemia detection.
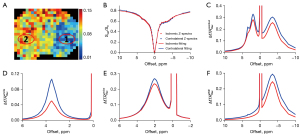
Figure 7 summarizes the comparisons of different APT quantification techniques. The stroke temporal evolution was assessed at 2, 6, and 24 h after reperfusion. Then, two ROIs (Figure 7D) were selected at each time point to calculate the CNR and CoV values for these quantification maps. The CNR comparisons are listed in Table 5, and the CoV comparisons are listed in Table 6. The MTRasym (3.5 ppm) method revealed little contrast between the ischemic and contralateral hemispheres within all time periods, while the other methods showed a visible contrast between the two hemispheres. However, in terms of the CNR and CoV metrics, performed the best among the methods at almost all time points.
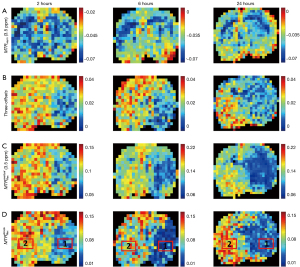
Table 5
| Time point | MTRasym(3.5 ppm) | Three-offsets | (3.5 ppm) | |
|---|---|---|---|---|
| 2 h | 0.49 | 3.11 | 3.08 | 3.9 |
| 6 h | 0.4 | 1.47 | 2.27 | 2.73 |
| 24 h | 0.32 | 1.96 | 4.58 | 3.93 |
Table 6
| Time point | MTRasym(3.5 ppm) | Three-offsets | (3.5 ppm) | |
|---|---|---|---|---|
| 2 h | 0.1894 | 0.4582 | 0.3274 | 0.181 |
| 6 h | 0.8216 | 0.4897 | 0.5169 | 0.2224 |
| 24 h | 0.7284 | 0.4606 | 0.4592 | 0.2897 |
Discussion
In this work, a Bayesian inference-based method solved by the MCMC algorithm was applied to the estimation and CEST effect fitting of multiple parameters. Using BM equations, we have verified the fitting performance of our approach in both simulated and in vivo studies. The results show that the method in this paper converges on good solutions, which describe the Z-spectra data well. The simulation results also show that if the available information allows unique solutions to be obtained, our method can conveniently and quickly obtain accurate parameter estimations. Experiments repeated under different parameter settings also illustrated the robustness of the method.
One of the major challenges of analyzing in vivo Z-spectra is the presence of multiple overlapping peaks that are distributed quite broadly (41). Several studies have been proposed to separate interfering signals, such as those of direct water saturation, MT, and NOE, from CEST effects. However, there are mixed exchangeable components present in the physiological environment. For example, in the stroke or tumor model, amine peaks from creatine can be observed (42,43). Due to the close resonance frequency, the fast exchanging amine pool (2 ppm) overlaps with the slow exchanging amide pool (3.5 ppm) (44). Therefore, it is difficult to separate the amide component of interest from the signal by adopting simple line-based methods during the usual APT analysis, which may lead to lower accuracy due to confounding by other effects.
Our experiments in ischemic stroke rats showed that the exchange effect of a pool can be quantified individually with the help of the BM equation after estimation of each parameter. They also demonstrated that purified effects perform better on contrast than mixed effects and facilitate analyses for specific effects individually. In comparisons of the various CEST spectra and residual spectra, amide spectra showed higher contrast than did mixed spectra. Thus, the APT map achieved the largest CNR and lowest CoV values.
The development of computer hardware and artificial intelligence techniques provides advanced tools for medical image analyses, especially complex models or high-dimensional computing. Previous CEST studies have applied machine learning (45) or neural network (23,46) methods. The present study takes advantage of the capabilities of the machine learning method MCMC, which generates high-dimensional distributions and iterative samplings to obtain a convergent sequence as parameter estimations that satisfy the model as much as possible.
The Bayesian inference theory permits prior information of the parameters to be included in the form of a probability distribution, which may reduce the risk of over-fitting and obtain faster convergence to the target when the prior knowledge is sufficiently accurate (47). However, if the assumptions of prior knowledge are excessively wrong, the results may be biased. To be safe, the prior values can be set to 0, thus ignoring the influence of prior probability.
An advantage of MCMC over alternative Bayesian inference class algorithms, such as variational methods, is its accuracy. This is because the variational method obtains an approximate solution by simplifying the original distribution (48), whereas MCMC seeks the true solution through iterative sampling. Compared with a previous study that used the probability model, we extended the 3-pool model to a more complex 5-pool model and achieved satisfactory results.
Due to the convenience of the MCMC method, we employed BM equations as our fitted model instead of the conventional line shape-based model. The BM model provides more physiological meaning, which gives insight into the underlying parameters and describes the multi-pool interaction process. Fitting a model based on BM equations to CEST spectra allows for the quantification of the metabolite concentration and exchange rate as well as simultaneous correction of field inhomogeneity, direct water saturation, and MT.
Despite its advantages, the MCMC process is time-consuming, which was one of the challenging issues that needed to be considered in our study. Further, as a homogeneous linear differential equation, the general solution of the BM model is complex. In contrast to simplified methods based on line shape, quantification based on BM equations requires more tissue parameters, which may necessitate a long scanning time (49). Moreover, in in vivo analysis, some parameters are difficult to determine. At the same time, the Monte Carlo simulation is a time-consuming method, with a significantly longer processing time than the least squares method used for traditional fitting. Therefore, an issue to be considered for the clinical use of this method in the future is its time cost, which for pixel-wise fitting is necessarily multiplied.
In response to this challenge, we adopted some simplification strategies in the bulk experiments, which mainly aimed to reduce the iterations and the amount of data. For the simulation and fitting models, a simplified approximate analytical solution model of the BM equations was applied to replace the general numerical solution. Previous research showed that the solution process of the BM numerical model was vastly more time-consuming than that of the modified model due to the complexity of its representation, while the accuracy of the BM model was comparable to that of the simplified model (50). To verify that the analytical solution model would not produce inaccurate results, we also evaluated its performance using a numerical solution as a fitting model on simulated data. Results of comparison, including Z-spectra fitting and CEST effect quantification, indicated that either the numerical solution or the analytical solution was a reliable model. The results are shown in Figure S3.
In in vivo images, there are usually no significant differences between the adjacent pixels except in regions at the edge of the lesion. Therefore, for the pixel-wise fitting process, we did not need to select the initial values randomly from uniform distributions for a new pixel. Instead, we were able to use the predicted values of the previous pixel as the initial estimations, which reduced useless iterations and accelerated the convergence speed. Accordingly, we have confirmed that reducing the number of iterations to approximately 500 is acceptable for rat experiments. For high-resolution images, downsampling can also serve as an alternative strategy to reduce the number of pixels (51), which can significantly reduce the time consumption despite some loss of resolution.
Besides the disadvantage of being time-consuming, the complexity of implementing MCMC is also a concern. The complicated processing flow increases the spatial complexity and the difficulty of understanding the results, which hinders the extension of the method to clinical application to some degree. Another limitation of this method is that the in vivo environment is much more complex than the theoretical model. First, there may be many more exchange effects than only amine and amide. Second, various interference effects, such as field inhomogeneities or motion artifacts, are factors that also need to be taken into account (52,53). Therefore, for different physiological scenarios, more parameters may need to be collected, the exchange pool model may need to be expanded, or additional preprocessing measures may need to be taken.
The effectiveness of the established model in our task suggests the potential of our method for future applications. First, as parameters of the BM equation, the MCMC method can also be used to fit B0/B1 values for field inhomogeneity correction. Second, for different diseases, through separate analysis of various exchange effects, we can find the most contrasting exchangeable protons among them. Therefore, the MCMC method can also be beneficial for exploring suitable biomarkers for specific application scenarios.
Conclusions
This study has demonstrated that an MCMC method combined with Bayesian inference theory can be used to solve BM equations, providing an alternative approach for accurate CEST quantification. This method shows promise for tissue parameter estimation and has wide potential in clinical disease diagnosis.
Acknowledgments
Funding: This work was supported in part by the National Natural Science Foundation of China (Nos. 61971350 and 82071914), the National Key R&D Program of China (No. 2019YFC1521101), and the Xi’an Science and Technology Bureau (No. 201805060ZD11CG44).
Footnote
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://qims.amegroups.com/article/view/10.21037/qims-22-313/coif). The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. This study was approved by the ethics board of Weifang Medical University in compliance with institutional guidelines for the care and use of animals.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Ward KM, Aletras AH, Balaban RS. A new class of contrast agents for MRI based on proton chemical exchange dependent saturation transfer (CEST). J Magn Reson 2000;143:79-87. [Crossref] [PubMed]
- van Zijl PC, Yadav NN. Chemical exchange saturation transfer (CEST): what is in a name and what isn't? Magn Reson Med 2011;65:927-48. [Crossref] [PubMed]
- Zhou JY, van Zijl PCM. Chemical exchange saturation transfer imaging and spectroscopy. Progress in Nuclear Magnetic Resonance Spectroscopy 2006;48:109-36. [Crossref]
- Zhang S, Malloy CR, Sherry AD. MRI thermometry based on PARACEST agents. J Am Chem Soc 2005;127:17572-3. [Crossref] [PubMed]
- Sun PZ, Wang E, Cheung JS. Imaging acute ischemic tissue acidosis with pH-sensitive endogenous amide proton transfer (APT) MRI--correction of tissue relaxation and concomitant RF irradiation effects toward mapping quantitative cerebral tissue pH. Neuroimage 2012;60:1-6. [Crossref] [PubMed]
- Sun PZ, Cheung JS, Wang E, Lo EH. Association between pH-weighted endogenous amide proton chemical exchange saturation transfer MRI and tissue lactic acidosis during acute ischemic stroke. J Cereb Blood Flow Metab 2011;31:1743-50. [Crossref] [PubMed]
- Zhou J, Wilson DA, Sun PZ, Klaus JA, Van Zijl PC. Quantitative description of proton exchange processes between water and endogenous and exogenous agents for WEX, CEST, and APT experiments. Magn Reson Med 2004;51:945-52. [Crossref] [PubMed]
- Longo DL, Cutrin JC, Michelotti F, Irrera P, Aime S. Noninvasive evaluation of renal pH homeostasis after ischemia reperfusion injury by CEST-MRI. NMR Biomed 2017; [Crossref] [PubMed]
- Tietze A, Blicher J, Mikkelsen IK, Østergaard L, Strother MK, Smith SA, Donahue MJ. Assessment of ischemic penumbra in patients with hyperacute stroke using amide proton transfer (APT) chemical exchange saturation transfer (CEST) MRI. NMR Biomed 2014;27:163-74. [Crossref] [PubMed]
- Walker-Samuel S, Ramasawmy R, Torrealdea F, Rega M, Rajkumar V, Johnson SP, Richardson S, Gonçalves M, Parkes HG, Arstad E, Thomas DL, Pedley RB, Lythgoe MF, Golay X. In vivo imaging of glucose uptake and metabolism in tumors. Nat Med 2013;19:1067-72. [Crossref] [PubMed]
- Jia G, Abaza R, Williams JD, Zynger DL, Zhou J, Shah ZK, Patel M, Sammet S, Wei L, Bahnson RR, Knopp MV. Amide proton transfer MR imaging of prostate cancer: a preliminary study. J Magn Reson Imaging 2011;33:647-54. [Crossref] [PubMed]
- Zhang Z, Zhang C, Yao J, Gao F, Gong T, Jiang S, Chen W, Zhou J, Wang G. Amide proton transfer-weighted magnetic resonance imaging of human brain aging at 3 Tesla. Quant Imaging Med Surg 2020;10:727-42. [Crossref] [PubMed]
- Foo LS, Harston G, Mehndiratta A, Yap WS, Hum YC, Lai KW, Mohamed Mukari SA, Mohd Zaki F, Tee YK. Clinical translation of amide proton transfer (APT) MRI for ischemic stroke: a systematic review (2003-2020). Quant Imaging Med Surg 2021;11:3797-811. [Crossref] [PubMed]
- Holt RW, Duerk JL, Hua J, Hurst GC. Estimation of Bloch model MT spin system parameters from Z-spectral data. Magn Reson Med 1994;31:122-30. [Crossref] [PubMed]
- Sun PZ, Zhou J, Sun W, Huang J, van Zijl PC. Suppression of lipid artifacts in amide proton transfer imaging. Magn Reson Med 2005;54:222-5. [Crossref] [PubMed]
- Jin T, Wang P, Zong X, Kim SG. MR imaging of the amide-proton transfer effect and the pH-insensitive nuclear overhauser effect at 9.4 T. Magn Reson Med 2013;69:760-70. [Crossref] [PubMed]
- Zaiss M, Schmitt B, Bachert P. Quantitative separation of CEST effect from magnetization transfer and spillover effects by Lorentzian-line-fit analysis of z-spectra. J Magn Reson 2011;211:149-55. [Crossref] [PubMed]
- Dixon WT, Ren J, Lubag AJ, Ratnakar J, Vinogradov E, Hancu I, Lenkinski RE, Sherry AD. A concentration-independent method to measure exchange rates in PARACEST agents. Magn Reson Med 2010;63:625-32. [Crossref] [PubMed]
- McMahon MT, Gilad AA, Zhou J, Sun PZ, Bulte JW, van Zijl PC. Quantifying exchange rates in chemical exchange saturation transfer agents using the saturation time and saturation power dependencies of the magnetization transfer effect on the magnetic resonance imaging signal (QUEST and QUESP): Ph calibration for poly-L-lysine and a starburst dendrimer. Magn Reson Med 2006;55:836-47. [Crossref] [PubMed]
- Zaiss M, Angelovski G, Demetriou E, McMahon MT, Golay X, Scheffler K. QUESP and QUEST revisited - fast and accurate quantitative CEST experiments. Magn Reson Med 2018;79:1708-21. [Crossref] [PubMed]
- Horská A, Spencer GS. Correctly accounting for radiofrequency spillover in saturation transfer experiments: application to measurement of the creatine kinase reaction rate in human forearm muscle. MAGMA 1997;5:159-63. [Crossref] [PubMed]
- Wolff SD, Balaban RS. Magnetization transfer contrast (MTC) and tissue water proton relaxation in vivo. Magn Reson Med 1989;10:135-44. [Crossref] [PubMed]
- Glang F, Deshmane A, Prokudin S, Martin F, Herz K, Lindig T, Bender B, Scheffler K, Zaiss M. DeepCEST 3T: Robust MRI parameter determination and uncertainty quantification with neural networks-application to CEST imaging of the human brain at 3T. Magn Reson Med 2020;84:450-66. [Crossref] [PubMed]
- McConnell HM. Reaction Rates by Nuclear Magnetic Resonance. J Chem Phys 1958;28:430-1. [Crossref]
- Murase K, Tanki N. Numerical solutions to the time-dependent Bloch equations revisited. Magn Reson Imaging 2011;29:126-31. [Crossref] [PubMed]
- Woessner DE, Zhang S, Merritt ME, Sherry AD. Numerical solution of the Bloch equations provides insights into the optimum design of PARACEST agents for MRI. Magn Reson Med 2005;53:790-9. [Crossref] [PubMed]
- Sun PZ. Simultaneous determination of labile proton concentration and exchange rate utilizing optimal RF power: Radio frequency power (RFP) dependence of chemical exchange saturation transfer (CEST) MRI. J Magn Reson 2010;202:155-61. [Crossref] [PubMed]
- Sun PZ. Simplified and scalable numerical solution for describing multi-pool chemical exchange saturation transfer (CEST) MRI contrast. J Magn Reson 2010;205:235-41. [Crossref] [PubMed]
- Chappell MA, Groves AR, Whitcher B, Woolrich MW. Variational Bayesian Inference for a Nonlinear Forward Model. IEEE Transactions on Signal Processing 2009;57:223-36. [Crossref]
- Jorgensen WL. Perspective on "Equation of state calculations by fast computing machines". Theor Chem Acc 2000;103:225-7. [Crossref]
- Beaumont MA, Zhang W, Balding DJ. Approximate Bayesian computation in population genetics. Genetics 2002;162:2025-35. [Crossref] [PubMed]
- Neal RM. Markov chain sampling methods for Dirichlet process mixture. Journal of Computational and Graphical Statistics 2000;9:249-65.
- WOOLF B. The log likelihood ratio test (the G-test); methods and tables for tests of heterogeneity in contingency tables. Ann Hum Genet 1957;21:397-409. [Crossref] [PubMed]
- Zaiss M, Zu Z, Xu J, Schuenke P, Gochberg DF, Gore JC, Ladd ME, Bachert P. A combined analytical solution for chemical exchange saturation transfer and semi-solid magnetization transfer. NMR Biomed 2015;28:217-30. [Crossref] [PubMed]
- Kim M, Gillen J, Landman BA, Zhou J, van Zijl PC. Water saturation shift referencing (WASSR) for chemical exchange saturation transfer (CEST) experiments. Magn Reson Med 2009;61:1441-50. [Crossref] [PubMed]
- Zivin JA. Diffusion-weighted MRI for diagnosis and treatment of ischemic stroke. Ann Neurol 1997;41:567-8. [Crossref] [PubMed]
- Parravano C, Baldeschwieler JD, Boudart M. Diffusion of water in zeolites. Science 1967;155:1535-6. [Crossref] [PubMed]
- Longa EZ, Weinstein PR, Carlson S, Cummins R. Reversible middle cerebral artery occlusion without craniectomy in rats. Stroke 1989;20:84-91. [Crossref] [PubMed]
- Zaiss M, Xu J, Goerke S, Khan IS, Singer RJ, Gore JC, Gochberg DF, Bachert P. Inverse Z-spectrum analysis for spillover-, MT-, and T1 -corrected steady-state pulsed CEST-MRI--application to pH-weighted MRI of acute stroke. NMR Biomed 2014;27:240-52. [Crossref] [PubMed]
- Hart HR Jr, Bottomley PA, Edelstein WA, Karr SG, Leue WM, Mueller O, Redington RW, Schenck JF, Smith LS, Vatis D. Nuclear magnetic resonance imaging: contrast-to-noise ratio as a function of strength of magnetic field. AJR Am J Roentgenol 1983;141:1195-201. [Crossref] [PubMed]
- Kikuchi K, Ishimatsu K, Zhang S, Dimitrov IE, Honda H, Sherry AD, Takahashi M. Presaturation Power Adjusted Pulsed CEST: A Method to Increase Independence of Target CEST Signals. Contrast Media Mol Imaging 2018;2018:3141789. [Crossref] [PubMed]
- Cai K, Singh A, Poptani H, Li W, Yang S, Lu Y, Hariharan H, Zhou XJ, Reddy R. CEST signal at 2ppm (CEST@2ppm) from Z-spectral fitting correlates with creatine distribution in brain tumor. NMR Biomed 2015;28:1-8. [PubMed]
- Taylor JM, Zhu XH, Zhang Y, Chen W. Dynamic correlations between hemodynamic, metabolic, and neuronal responses to acute whole-brain ischemia. NMR Biomed 2015;28:1357-65. [Crossref] [PubMed]
- Zhang XY, Wang F, Li H, Xu J, Gochberg DF, Gore JC, Zu Z. Accuracy in the quantification of chemical exchange saturation transfer (CEST) and relayed nuclear Overhauser enhancement (rNOE) saturation transfer effects. NMR Biomed 2017; [Crossref] [PubMed]
- Goldenberg JM, Cárdenas-Rodríguez J, Pagel MD. Machine learning improves classification of preclinical models of pancreatic cancer with chemical exchange saturation transfer MRI. Magn Reson Med 2019;81:594-601. [Crossref] [PubMed]
- Zaiss M, Deshmane A, Schuppert M, Herz K, Glang F, Ehses P, Lindig T, Bender B, Ernemann U, Scheffler K. DeepCEST: 9.4 T Chemical exchange saturation transfer MRI contrast predicted from 3 T data - a proof of concept study. Magn Reson Med 2019;81:3901-14. [Crossref] [PubMed]
- Chappell MA, Donahue MJ, Tee YK, Khrapitchev AA, Sibson NR, Jezzard P, Payne SJ. Quantitative Bayesian model-based analysis of amide proton transfer MRI. Magn Reson Med 2013;70:556-67. [Crossref] [PubMed]
- Attias H, editor. A variational Bayesian framework for graphical models. 13th Annual Conference on Neural Information Processing Systems (NIPS); 1999 Nov 29-Dec 04; Co2000.
- Xiao G, Sun PZ, Wu R. Fast simulation and optimization of pulse-train chemical exchange saturation transfer (CEST) imaging. Phys Med Biol 2015;60:4719-30. [Crossref] [PubMed]
- Kujawa A, Kim M, Demetriou E, Anemone A, Livio Longo D, Zaiss M, Golay X. Assessment of a clinically feasible Bayesian fitting algorithm using a simplified description of Chemical Exchange Saturation Transfer (CEST) imaging. J Magn Reson 2019;300:120-34. [Crossref] [PubMed]
- Zhou IY, Wang E, Cheung JS, Zhang X, Fulci G, Sun PZ. Quantitative chemical exchange saturation transfer (CEST) MRI of glioma using Image Downsampling Expedited Adaptive Least-squares (IDEAL) fitting. Sci Rep 2017;7:84. [Crossref] [PubMed]
- Zaiss M, Herz K, Deshmane A, Kim M, Golay X, Lindig T, Bender B, Ernemann U, Scheffler K. Possible artifacts in dynamic CEST MRI due to motion and field alterations. J Magn Reson 2019;298:16-22. [Crossref] [PubMed]
- Schuenke P, Windschuh J, Roeloffs V, Ladd ME, Bachert P, Zaiss M. Simultaneous mapping of water shift and B1 (WASABI)-Application to field-Inhomogeneity correction of CEST MRI data. Magn Reson Med 2017;77:571-80. [Crossref] [PubMed]


