Incorporating multiple magnetic resonance diffusion models to differentiate low- and high-grade adult gliomas: a machine learning approach

Introduction

Glioma is the most common neuroepithelial tumor of the cerebral nervous system and is classified into four grades by the World Health Organization (1,2). Low- (LGG) (grade II) and high-grade gliomas (HGG) (grades III and IV) differ in pathology and prognosis. In patients for whom an invasive procedure is considered feasible, the glioma grade is determined using stereotactic biopsy followed by histopathological analysis. However, the limitations of invasive procedures can lead to sampling errors, which can compromise the accuracy of diagnosis and the significant risks may be associated with the invasive procedure in some cases (3). Therefore, glioma grading through noninvasive medical imaging methods is needed to overcome these limitations.

Several previous studies have proposed grading gliomas based on quantitative parameters of magnetic resonance imaging (MRI) techniques, such as magnetic resonance (MR) spectroscopy, perfusion imaging, T2 mapping, and diffusion-weighted imaging (DWI). Of these methods, DWI is the most sensitive and has great potential for grading tasks (4-8). Many DWI models have been proposed over the past few years. One diffusion parameter, the apparent diffusion coefficient (ADC), is used to describe free diffusion with a monoexponential function, where the distribution of molecular displacements obeys a Gaussian law (9,10). However, different diffusion compartments may arise from the complex structure of tumor tissues (11-14). As a result, the diffusion displacement probability distribution can deviate substantially from Gaussian law (11). To overcome this dilemma, models incorporating multiple water diffusion components have been developed (11,15-18). For example, Le Bihan et al. (17) proposed the intravoxel incoherent motion (IVIM) model, which separates simple diffusion and microvascular perfusion in tissues. Bennett et al. (15) proposed the stretched-exponential model (SEM) and showed that signal attenuation is consistent with a multicompartmental theory of water diffusion in the brain. A statistical model (SM) to describe a considerable amount of diffusion-attenuated MR signals in biological systems has also been published (19). Diffusion kurtosis imaging (DKI) has previously been used to evaluate non-Gaussian water diffusion in bodily tissues (11,20), and in recent years, two advanced DWI models to measure tissue heterogeneity have also been proposed. Using a fractional order calculus (FROC) diffusion model has been shown to improve the accuracy of MR imaging in differentiating benign and malignant pediatric brain tumors and grading adult gliomas (9,21). Significant differences between malignant and benign pediatric tumors have also been observed using the continuous-time random walk (CTRW) model (22). However, these models have not been tested for reproducibility with other test sets, nor has the value of combining multiple DWI models in glioma grading been discussed (23). Therefore, it would be helpful to investigate whether combining multiple DWI models can improve their performance in grading gliomas.

Previous studies have utilized multimodality MRI radiomics with machine learning (ML) approaches to classify gliomas, demonstrating that DWI features might improve diagnostic accuracy (24,25). The results of one study showed that incorporating diffusion-weighted MRI into an ML-based radiomics model could improve the diagnosis of pseudoprogression in patients with glioblastoma (5). Another study also highlighted the potential of diffusion MR with radiomics analysis in the evaluation of glioma malignancy (26). Based on this prior work, we hypothesized that combining multiple DWI models with ML algorithms might improve the performance of DWIs in differentiating glioma grades.

In this study, information extracted from multiple diffusion models was combined and subjected to ML-based analysis to improve the performance of diffusion imaging in glioma grading. Further, the robustness of the proposed method was compared with that of the traditional single DWI model and DWI radiomics, and the results of these comparisons are presented herein. We present the following article in accordance with the TRIPOD reporting checklist (available at https://qims.amegroups.com/article/view/10.21037/qims-22-145/rc).

Methods

The current study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). The institutional review boards of Hua Shan Hospital affiliated with Fudan University and Ren Ji Hospital affiliated with Shanghai Jiao Tong University approved this retrospective study and waived the requirement to obtain informed consent.

Core codes are available at https://github.com/Arroway-JQ/combined-DWI-modeling-and-tumor-classification.

Patients

This study recruited 147 adult patients with gliomas from Hua Shan Hospital affiliated with Fudan University between 2014 and 2015. A further 69 patients were recruited from Ren Ji Hospital affiliated with Shanghai Jiao Tong University between 2016 and 2019 as an external test cohort.

The inclusion criteria for the study were as follows: (I) three types of MRI images [T1-weighted images with enhancement (T1WI+C), T2-weighted fluid-attenuated inversion recovery (T2W-FLAIR), and DWI] were available for evaluation; (II) surgery was performed for a pathologic diagnosis after MR imaging and integrated clinical information was obtained; (III) the DWI scan was performed using the correct number of b-values (21 for the first dataset and 17 for the second). After these criteria had been applied, the primary dataset consisted of 74 patients (18–75 years old), including 15 patients as the internal test set. Of the patients in the primary dataset, 37 had LGG and 37 had HGG according to the World Health Organization classification (2). The external test set comprised 55 patients (14–78 years old), of whom 25 patients had LGGs, with the remaining patients having HGGs.

Acquisition of MRI scans

The MRI scans (T1WI+C, T2W-FLAIR, and DWI sequences) were performed on two 3.0 tesla scanners (MR750, Signa HDxt, GE Medical System, Milwaukee, WI, USA) using a standard eight-channel phased-array head coil. The DWI was acquired using a single-shot spin-echo planar imaging sequence with 21 and 17 b-values at Hua Shan Hospital and Ren Ji Hospital, respectively. Diffusion gradients were applied in all three orthogonal directions (x-, y-, and z-axes) to obtain a trace-weighted image to minimize the influence of diffusion anisotropy. Other core image acquisition parameters are shown in Figure 1.

Figure 1 Flowchart of the study inclusion and exclusion process. ^†, 21 b-value: 0, 10, 20, 30, 50, 100, 150, 200, 300, 400, 500, 600, 800, 1,000, 1,500, 2,000, 2,500, 3,000, 3,500, 4,000, and 4,500 s/mm². Other core image acquisition parameters for Hua Shan Hospital were as follows: partial Fourier, average times NEX =2 (=4 for b =3,500–4,500 s/mm²), TR =5,000 ms, TE =90.6 ms, separation between two diffusion gradient lobes Δ =42.688 ms, duration of each diffusion gradient δ =29.404 ms, slice thickness =4 mm, acquisition matrix size =128×128 zeros-padded to 256×256, flip angle =90° and pixel size =1×1 mm²; ^‡, 17 b-value: 0, 20, 50, 80, 150, 200, 300, 500, 800, 1,000, 1,500, 2,000, 2,500, 3,000, 3,500, 4,000, and 4,500 s/mm². Other core image acquisition parameters for Ren Ji Hospital were as follows: partial Fourier, acceleration =2, TR =3,000 ms, TE =105.8 ms, separation between two diffusion gradient lobes Δ =42.688 ms, duration of each diffusion gradient δ =29.404 ms, slice thickness =6 mm, acquisition matrix size =192×192, flip angle =90°, and pixel size =1×1 mm². DWI, diffusion-weighted imaging; TR, repetition time; TE, echo time.

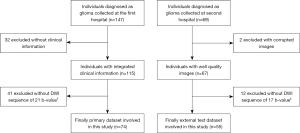
Image preprocessing

The entire process for building the prediction model is shown in Figure 2.

Figure 2 Flow chart for all the procedures to predict LGG and HGG in this study. The first stage is image processing, including DWI model building and parameter mapping. The second stage is ML-based model building. In this part, seven histogram features were extracted and selected using a five-step procedure: a two-sided Wilcoxon-Mann-Whitney U-test, ML feature selection, a voting system, a correlation test, and feature combination. Prediction models were trained and selected in the primary dataset. The third stage included validation and evaluation of our proposed model and traditional DWI models in the internal and external cohorts. DWI, diffusion-weighted imaging; ROI, region of interest; ADC, apparent diffusion coefficient; IVIM, intravoxel incoherent motion; SEM, stretched-exponential model; FROC, fractional order calculus; CTRW, continuous-time random walk; DKI, diffusion kurtosis imaging; SM, statistical model; ML, machine learning; LR, logistic regression; SVM, support-vector machine; KNN, K-nearest neighbors; NB, naïve Bayes; RF, random forests; AUC, area under the curve; LGG, low-grade glioma; HGG, high-grade glioma.

The diffusion images were eddy-current corrected, and the skulls were removed through MRI tools using the Functional Magnetic Resonance Imaging of the Brain Software Library (FSL) (27). Subsequently, a median filter was used to smoothen and denoise the images. The diffusion-attenuated signals were acquired at the voxel level, and then the signal intensity was normalized to the signal intensity of the b0 image.

With reference to T1WI+C images, two radiologists placed regions of interest (ROIs) on the solid part of tumors on the b =0 DWI images, avoiding necrosis, edema, and hemorrhage. The ROIs were then propagated to each slice of the parameter maps. For the external test set, a single radiologist at the second hospital read the diffusion images of multiple b-values, and the diagnostic accuracy was 0.71 (39 of 55 cases were predicted the same as the ground truth) with an area under the receiver operating characteristic (ROC) curve (AUC) of 0.71 (95% confidence interval: 0.57–0.86).

Multi-DWI models

Based on the above theories, the present study applied seven diffusion models (ADC, IVIM, SEM, SM, DKI, FROC, and CTRW) using MATLAB (MathWorks, Inc., 2019b, Natick, MA, USA).

The monoexponential model is described as Eq. [1], where S denotes the signal intensity with diffusion sensitization, and S₀ denotes the signal intensity without sensitization.

S=S0exp(−b×ADC)[1]

The IVIM model was fitted according to Eq. [2], where f is the perfusion fraction; D_f is the pseudodiffusion coefficient, which represents faster diffusion; and D_s is the actual diffusion coefficient, which represents slower diffusion (28).

S=S0(fexp(−bDf)+(1−f)exp(−bDs))[2]

The SEM model is presented as Eq. [3], where α∈(0,1) represents the deviation of the signal attenuation (15), and DDC is the distributed diffusion coefficient.

S=S0exp(−(b×DDC)α)[3]

The SM model is described as Eq. [4], where σ is the distribution width and ADC_S is the position of the distribution maxima (19).

S=S0exp(−bADCS+12σ2b2)[4]

The DKI model was applied according to Eq. [5] using additional information on the diffusion kurtosis K.

S=S0exp(−bDK+16b2DK2K)[5]

The FROC model is presented as Eq. [6], where δ is the diffusion gradient pulse width, Δ is the gradient lobe separation, β_f^* correlates with tissue heterogeneity, and µ is the microstructural quantity (21).

S=S0exp{−Dμ2(βf*−1)(bΔ−δ/3)βf*(Δ−2βf*−12βf*+1δ)}[6]

The CTRW model was written using the Mittag-Leffler function (MLF) as in Eq. [7], where D_c denotes the anomalous diffusion coefficient, α_c and β_c represent the diffusion heterogeneity of time and space (22), respectively.

S=S0Eαc(−(bDc)βc)[7]

All DWI models were applied voxel by voxel with the R-squared (R²) value recorded to evaluate the goodness of fit. The ADC, SM, and DKI models were calculated using polynomial fitting, and the others were fitted by applying the Levenberg-Marquardt algorithm (29). In total, 16 parameters were derived from the seven models (ADC, f, D_s, D_f, DDC, α, ADC_S, σ, D_K, K, D, µ, β_f^*, D_c, β_c, α_c).

Feature extraction

The primary dataset was randomly stratified into training (n=59) and test (n=15) sets at a ratio of 8 to 2. Five randomly permuted five-fold cross-validations were used to evaluate our method. Balance of the training and test data was considered. Thus, the ratio of HGGs and LGGs was maintained between the training, validation, and test sets. An external test data set (n=55) from another medical center was also included for another verification.

The DWI signals of ROIs were filtered by ranking their R² value from curve fitting, retaining only the top 95% of voxels for each tumor. The mean, maximum, minimum, median, kurtosis, skewness, and variance values were calculated for each parameter and each patient in the primary and external datasets. In all, our model extracted 112 (16×7) features from each case.

The DWI radiomic features were extracted using the PyRadiomics package in Python software (v. 3.6, Python Software Foundation, Wilmington, DE, USA, https://www.python.org/) (30). Feature scaling was performed on both the primary and external datasets using Z-score transformation (31). In this study, 7,076 and 6,100 features were extracted from each case in the primary dataset and the external test set, respectively (Appendix 1).

Feature selection

All work in this section was accomplished using an open ML library and scikit-learn (ver. 0.22) in Python (32). The clinical information for the training and test datasets is shown in Table 1.

Feature selection was performed on five-fold cross-validation sets. A rigorous five-step process (Figure 2) was implemented to select significant features and avoid collinearity. A two-sided Wilcoxon-Mann-Whitney U-test was performed to identify features which were significantly different (P<0.05) between HGGs and LGGs for subsequent analysis. Then, the most significant features (votes >9/2) were selected using nine ML methods: logistic regression, support-vector machine, K-nearest neighbors, random forest for a single feature, random forest for all features, naïve Bayes, stacking, recursive-feature elimination, and Least Absolute Shrinkage and Selection Operator (see Figure S1). After that, the retained features were subjected to correlation tests to eliminate potentially collinear features (r>0.70), which introduce redundant information to the prediction model (Table S1). Finally, the features were combined into subgroups based on their corresponding DWI models (Table S2).

The feature subgroups based on the single DWI model consisted of the mean value of each parameter without undergoing ML selection (see Appendix 2, which describes the feature selection for the two other DWI methods).

Training and estimator selection

Six estimators (logistic regression, support-vector machine, K-nearest neighbors, random forest, naïve Bayes, and stacking) were used to construct the classification models and to learn how best to combine the predictions from the above base machine as the new features. They were reclassified with logistic regression as a metaclassifier. Stacking is an ensemble ML algorithm that uses meta-learning. The benefit of stacking is that it can harness the capabilities of a range of well-performing models by using their output as input and ultimately achieve a better predictive performance than any single model in the ensemble (33). For each estimator, a grid search was conducted for automatic parameter tuning.

Prediction models were first trained in the five-fold cross-validation set (34). Then, the final prediction models for the three classification methods were selected based on the highest AUC in the internal test set (see Table S3 for integrated training and internal testing results).

Testing and comparisons

Internal and external test sets were included to evaluate the performances of the single DWI, DWI radiomics, and ML-based multiparametric DWI prediction models. To determine the models’ accuracy, the AUCs were calculated as evaluation indices. The cutoff values that provided the best sensitivity and specificity were determined according to the maximum value of the Youden index (35). Differences between the three models were compared. The AUCs of the three models were compared using the DeLong test (36-38).

Results

Multimodel DWI fitting

The DWI signal attenuation curves were fitted based on the theoretical bases of the seven diffusion models. Figure 3 shows the maps of the 16 parameters obtained compared to b0 images of an LGG and an HGG.

Figure 3 Sixteen parameter maps for HGG and LGG cases. The images in sequence are: b₀ map; ADC map; DDC map and α map for SEM; ADC_S map and σ map for SM; f map, D_s map, and D_f map for IVIM model; D map, β_f^*map, and μ map for FROC model; D_Cmap, α_c map, and β_c map for CTRW model; and D_K map and K map for DKI model. ADC, apparent diffusion coefficient; HGG, high-grade glioma; LGG, low-grade glioma; SEM, stretched-exponential model; SM, statistical model; IVIM, intravoxel incoherent motion; FROC, fractional order calculus; CTRW, continuous-time random walk; DKI, diffusion kurtosis imaging.

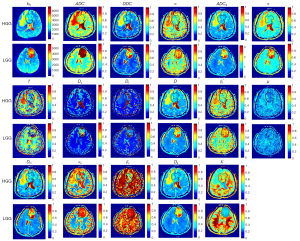
The SEM, FROC, and CTRW models outperformed the other models (Table S4), with R²_mean 0.9959, 0.9788, and 0.9801, respectively. The R² values of the SM and DKI models were similar, while those of ADC and IVIM models were relatively lower than the other models (<0.96).

Significant features

After five-step feature selection, only ten features were selected as significant. The subgroups of these features and combination descriptions are shown in Table 2 and Table S2. Based on DWI radiomics analysis, five sequential texture features and four wavelet transformations were selected after a similar feature selection process. For the construction of the single DWI prediction model, only the mean values of parameters were chosen (see Table S5, which demonstrates the feature combinations of the two established DWI methods).

Optimal prediction models

Figure 4A shows the ROC curves of cross-validations of the combined SEM, CTRW, and FROC (SCF) model containing seven features (SEM model with DDC_min and α_skewness, CTRW model with α_c_kurtosis, α_c_variance and β_c_variance, and FROC model with β_f^* min and µ_skewness as features). Then, the fourth-fold stack estimator for SCF was chosen as the final prediction model.

Figure 4 ROC curves of different models in the internal test and external validation sets. (A) The ROC curve of five randomly permuted five-fold cross-validation sets using SCF as input and stack as the estimator. (B) The ROC curve of feature combinations based on the multiparametric DWI model and ML selection in the internal test set. (C) The ROC curve of feature combinations based on the single DWI models in the internal test set. (D) The ROC curve of feature combinations based on DWI radiomics in the internal test set. ROC, receiver operating characteristic; SCF, SEM, CTRW, and FROC models; AUC, area under the curve; F, FROC model; SI, SEM and IVIM models; SC, SEM and CTRW models; SCs, SEM, CTRW, and statistic models; LR, logistic regression; RF, random forest; ADC, apparent diffusion coefficient; SM, statistical model; SEM, stretched-exponential model; DKI, diffusion kurtosis imaging; FROC, fractional order calculus; IVIM, intravoxel incoherent motion; CTRW, continuous-time random walk; DWI, diffusion-weighted imaging; ML, machine learning.

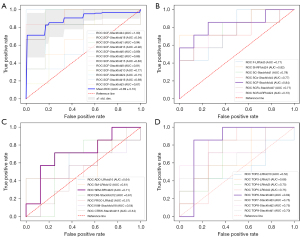
As shown in Figure 4B, the SCF model had the highest AUC (0.84) (sensitivity =0.86 and specificity =0.75) in the internal test set. Figure 4C shows that the SEM model had the highest AUC value (0.71) among the single DWI models. Furthermore, the subgroup TOP6 had the best performance (AUC =0.84) among the DWI radiomics features, as shown in Figure 4D and Table S6. Both the SCF model and the radiomics model significantly improved the predictive performance of the single DWI model (P=8.60×10⁻⁴, 1.90×10⁻⁴ for DeLong test, respectively).

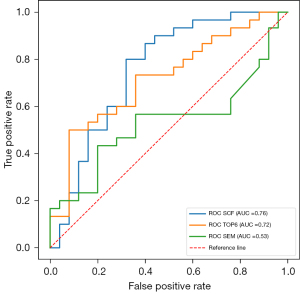
Compared with the established methods, our method performed better in the external cohort. As shown in Table 3, in the external cohort, the SCF model showed both a higher accuracy and AUC value than the SEM (DDC_mean and α_mean in SEM model) and TOP6 models (accuracy =0.76, 0.53, and 0.67, respectively). Table 4 shows that the SCF model performed significantly better in classifying the external test set than did the SEM model (AUC =0.76 and 0.53, respectively, P=0.02 for the DeLong test). The AUC of the SCF model was higher than that of the DWI radiomics model, but the difference was not significant (AUC =0.72, P=0.61 for the DeLong test) (Figure 5).

Figure 5 ROC curves of the multiparametric DWI model, the single DWI model, and the DWI radiomics model in the external test set. ROC, receiver operating characteristic; SCF, SEM, CTRW, and FROC models; AUC, area under the curve; SEM, stretched-exponential model; DWI, diffusion-weighted imaging; CTRW, continuous-time random walk; FROC, fractional order calculus.

Discussion

In this study, a multiparametric DWI model to differentiate LGGs and HGGs was proposed. We used images with multiple high b-values to extract higher-order features from 16 parameters derived from seven DWI models proposed in previous studies (7,15,17,19-22). Features were selected by using ML algorithms and statistical analyses. We found that the SCF prediction model performed best in both the primary dataset and the external test set. The robustness of our method was evaluated in the external test set and compared with that of other methods, and the proposed method was found to have advantages over the two established DWI methods.

Multiparametric DWI model

Based on different approaches to diffusion imaging, seven DWI models were incorporated into our model. As shown in Figure 3, the ADC, DDC, Dc, D, ADC_S, and D_K maps share similar areas of contrast, reflecting similar water diffusion distribution in the tissues, whereas the α, β*_f, α_c, and β_c maps show tissue heterogeneity; these findings are consistent with results from previous studies (21,22). The SEM and CTRW models reflected microstructure characteristics better with high b values than other models and thus, had better fitting quality for signal attenuation (R²=0.9959, 0.9801, respectively, see Table S4). In line with the findings of Niendorf et al. (18), the monoexponential model had the worst performance of all the models, with the fitted curve noticeably deviating from the original curve in the high b-value region.

In this study, the ML approach was used, and features from multiple DWI models were combined. Due to the incorporation of multiple features into our model, the problem of overfitting had to be considered. To mitigate the risk of overfitting, we adopted two preventive measures. The first was the use of a rigorous five-step feature selection procedure with a reduced number of features. The second was the use of independent internal and external test data sets.

Comparisons with established DWI methods

Instead of focusing on multimodality radiomics, this work focused on investigating and improving the diagnostic potency of DWI models. Our study demonstrated that multimodel DWI was useful, with our results being comparable to those of another multimodality radiomics study, in which the AUC of the external cohort was 0.75 (34). We agree that advanced MRI sequences like diffusion imaging can provide meticulous radiologic information about glioma and may be suitable for a predictive model (5). Many previous studies have demonstrated the resolving ability of single DWI models. For example, one study reported the value of DKI with radiomics in grading gliomas (26). However, further investigation using a larger sample and an external test set is still needed. Compared with models in two previous studies focusing on diffusion MRI in glioma grading (accuracy =0.80, 0.82) (9,39), our model performed better in cross-validation sets (accuracy =0.91), and neither of these studies included an independent test set. Furthermore, the repeatability of our multiparametric DWI model was demonstrated in both the internal and external test sets. In this study, the AUCs of the multiparametric DWI model and the radiomics model were significantly higher (P<0.05) than that of the single DWI model (AUC =0.73) in the internal test set. As shown in Table 3, the single DWI model showed a sharp decrease in performance in the external test set (AUC =0.53), while our multiparametric DWI model showed a superior performance in the external test set (AUC =0.76, P=0.02). These results indicate that measuring the mean value of parameters within ROIs in tissues based on the single DWI model might fail to sufficiently capture the tumor complexity; thus, this method would have limited applicability to other datasets.

Although the SCF (our method) and TOP6 (the DWI radiomics method) models had comparable accuracy (0.80, P>1) in the internal test set, the accuracy of the SCF model (0.76) was much higher than that of the TOP6 model (0.67) in the external test set. The AUC values of the SCF model in the external test set were decreased compared to those in the internal test set on account of the decreasing of specificity in the external test set. But, the sensitivity remained high at 0.80. The accuracy and AUC value of the SCF model were higher than those of the DWI radiomics model in the external test set; however the AUC showed no significant difference between the two models. Also, compared to that in the internal test set, the sensitivity of the DWI radiomics model in the external test set decreased substantially to 0.5, while the specificity remained high at 0.92. Our findings demonstrate that quantitative analysis using our multiparametric DWI model may be more generalizable than signal analysis of images (the DWI radiomics model).

Our study has several limitations. First, differences in scanning parameters, such as b-values and the echo time (TE), between the training and external sets may have introduced biases which impacted the accuracy of the external test set results. In our study, the accuracy of the SCF model decreased by 0.04 in the external test set relative to the internal test set, although we used feature scaling (32), applied a regularization algorithm for feature selection, and used cross-validation to evaluate the model’s generalization error and to select the estimator (40,41). Subsequent studies should be conducted by augmenting the number of samples, and a standard methodology of normalization between different cohorts also needs further investigation. Furthermore, the DWI data in this work were collected in three orthogonal directions, which did not meet the requirements for computing some of the direction-dependent matrices, such as k⊥ and k∥, in the DKI model. The limited diffusion directions could have affected the isotropic K, which may be one of the reasons for the poor performance of the DKI model. Also, multiple diffusion directions, if clinically available, make it possible to analyze other diffusion models, such as neurite orientation dispersion and density imaging, diffusion basis spectrum imaging, and constrained diffusional variance decomposition models (42-44).

Conclusions

In conclusion, our multiparametric DWI model with an ML algorithm was found to be feasible and valuable for predicting LGGs and HGGs. Multiple DWI parameters can provide abundant critical information for clinical diagnosis. Compared to that of the single DWI model, the performance of the SCF model in glioma classification was significantly improved (P<0.05), with our model achieving higher accuracy and AUC values in both the internal (accuracy =0.80, AUC =0.84) and external (accuracy =0.76, AUC =0.76) test sets.

In summary, our method is credible and robust for differentiating LGGs and HGGs in adults. The promising results of this study will pave the way for further research combining other diffusion models and involving larger patient groups.

Acknowledgments

Funding: This work was supported by the National Natural Science Foundation of China (No. 81971583 to HW), Shanghai Natural Science Foundation (No. 20ZR1406400 to HW), Science and Technology Support Project for Medicine sponsored by Science and Technology Commission of Shanghai Municipality (No. 18411967300 to HW), and Shanghai Municipal Science and Technology Major Project (Nos. 2017SHZDZX01 and 2018SHZDZX01 to HW).

Footnote

Reporting Checklist: The authors completed the TRIPOD reporting checklist. Available at https://qims.amegroups.com/article/view/10.21037/qims-22-145/rc

Conflicts of Interest: All authors completed the ICMJE uniform disclosure form (available at https://qims.amegroups.com/article/view/10.21037/qims-22-145/coif). The authors have no conflicts of interest to declare.

Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The current study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). The institutional review boards of Hua Shan Hospital affiliated with Fudan University and Ren Ji Hospital affiliated with Shanghai Jiao Tong University approved this retrospective study, and the requirement to obtain informed consent was waived.

Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.

References

1. Bray F, Ferlay J, Soerjomataram I, Siegel RL, Torre LA, Jemal A. Global cancer statistics 2018: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries. CA Cancer J Clin 2018;68:394-424. [Crossref] [PubMed]
2. Louis DN, Perry A, Reifenberger G, von Deimling A, Figarella-Branger D, Cavenee WK, Ohgaki H, Wiestler OD, Kleihues P, Ellison DW. The 2016 World Health Organization Classification of Tumors of the Central Nervous System: a summary. Acta Neuropathol 2016;131:803-20. [Crossref] [PubMed]
3. Jackson RJ, Fuller GN, Abi-Said D, Lang FF, Gokaslan ZL, Shi WM, Wildrick DM, Sawaya R. Limitations of stereotactic biopsy in the initial management of gliomas. Neuro Oncol 2001;3:193-200. [Crossref] [PubMed]
4. Provenzale JM, Mukundan S, Barboriak DP. Diffusion-weighted and perfusion MR imaging for brain tumor characterization and assessment of treatment response. Radiology 2006;239:632-49. [Crossref] [PubMed]
5. Kim JY, Park JE, Jo Y, Shim WH, Nam SJ, Kim JH, Yoo RE, Choi SH, Kim HS. Incorporating diffusion- and perfusion-weighted MRI into a radiomics model improves diagnostic performance for pseudoprogression in glioblastoma patients. Neuro Oncol 2019;21:404-14. [Crossref] [PubMed]
6. Kono K, Inoue Y, Nakayama K, Shakudo M, Morino M, Ohata K, Wakasa K, Yamada R. The role of diffusion-weighted imaging in patients with brain tumors. AJNR Am J Neuroradiol 2001;22:1081-8. [PubMed]
7. Bulakbasi N, Guvenc I, Onguru O, Erdogan E, Tayfun C, Ucoz T. The added value of the apparent diffusion coefficient calculation to magnetic resonance imaging in the differentiation and grading of malignant brain tumors. J Comput Assist Tomogr 2004;28:735-46. [Crossref] [PubMed]
8. Gu W, Fang S, Hou X, Ma D, Li S. Exploring diagnostic performance of T2 mapping in diffuse glioma grading. Quant Imaging Med Surg 2021;11:2943-54. [Crossref] [PubMed]
9. Sui Y, Xiong Y, Jiang J, Karaman MM, Xie KL, Zhu W, Zhou XJ. Differentiation of Low- and High-Grade Gliomas Using High b-Value Diffusion Imaging with a Non-Gaussian Diffusion Model. AJNR Am J Neuroradiol 2016;37:1643-9. [Crossref] [PubMed]
10. Le Bihan D. The‘’wet min’’: water and functional neuroimaging. Phys Med Biol 2007;52:R57-90. [Crossref] [PubMed]
11. Jensen JH, Helpern JA, Ramani A, Lu H, Kaczynski K. Diffusional kurtosis imaging: the quantification of non-gaussian water diffusion by means of magnetic resonance imaging. Magn Reson Med 2005;53:1432-40. [Crossref] [PubMed]
12. Le Bihan D. Intravoxel incoherent motion perfusion MR imaging: a wake-up call. Radiology 2008;249:748-52. [Crossref] [PubMed]
13. Wáng YXJ. Mutual constraining of slow component and fast component measures: some observations in liver IVIM imaging. Quant Imaging Med Surg 2021;11:2879-87. [Crossref] [PubMed]
14. Wáng YXJ. A reduction of perfusion can lead to an artificial elevation of slow diffusion measure: examples in acute brain ischemia MRI intravoxel incoherent motion studies. Ann Transl Med 2021;9:895. [Crossref] [PubMed]
15. Bennett KM, Schmainda KM, Bennett RT, Rowe DB, Lu H, Hyde JS. Characterization of continuously distributed cortical water diffusion rates with a stretched-exponential model. Magn Reson Med 2003;50:727-34. [Crossref] [PubMed]
16. Le Bihan D. Looking into the functional architecture of the brain with diffusion MRI. Nat Rev Neurosci 2003;4:469-80. [Crossref] [PubMed]
17. Le Bihan D, Breton E, Lallemand D, Aubin ML, Vignaud J, Laval-Jeantet M. Separation of diffusion and perfusion in intravoxel incoherent motion MR imaging. Radiology 1988;168:497-505. [Crossref] [PubMed]
18. Niendorf T, Dijkhuizen RM, Norris DG, van Lookeren Campagne M, Nicolay K. Biexponential diffusion attenuation in various states of brain tissue: implications for diffusion-weighted imaging. Magn Reson Med 1996;36:847-57. [Crossref] [PubMed]
19. Yablonskiy DA, Bretthorst GL, Ackerman JJ. Statistical model for diffusion attenuated MR signal. Magn Reson Med 2003;50:664-9. [Crossref] [PubMed]
20. Wang X, Gao W, Li F, Shi W, Li H, Zeng Q. Diffusion kurtosis imaging as an imaging biomarker for predicting prognosis of the patients with high-grade gliomas. Magn Reson Imaging 2019;63:131-6. [Crossref] [PubMed]
21. Sui Y, Wang H, Liu G, Damen FW, Wanamaker C, Li Y, Zhou XJ. Differentiation of Low- and High-Grade Pediatric Brain Tumors with High b-Value Diffusion-weighted MR Imaging and a Fractional Order Calculus Model. Radiology 2015;277:489-96. [Crossref] [PubMed]
22. Karaman MM, Sui Y, Wang H, Magin RL, Li Y, Zhou XJ. Differentiating low- and high-grade pediatric brain tumors using a continuous-time random-walk diffusion model at high b-values. Magn Reson Med 2016;76:1149-57. [Crossref] [PubMed]
23. Bai Y, Lin Y, Tian J, Shi D, Cheng J, Haacke EM, Hong X, Ma B, Zhou J, Wang M. Grading of Gliomas by Using Monoexponential, Biexponential, and Stretched Exponential Diffusion-weighted MR Imaging and Diffusion Kurtosis MR Imaging. Radiology 2016;278:496-504. [Crossref] [PubMed]
24. Qin JB, Liu Z, Zhang H, Shen C, Wang XC, Tan Y, Wang S, Wu XF, Tian J. Grading of Gliomas by Using Radiomic Features on Multiple Magnetic Resonance Imaging (MRI) Sequences. Med Sci Monit 2017;23:2168-78. [Crossref] [PubMed]
25. Su C, Jiang J, Zhang S, Shi J, Xu K, Shen N, Zhang J, Li L, Zhao L, Zhang J, Qin Y, Liu Y, Zhu W. Radiomics based on multicontrast MRI can precisely differentiate among glioma subtypes and predict tumour-proliferative behaviour. Eur Radiol 2019;29:1986-96. [Crossref] [PubMed]
26. Takahashi S, Takahashi W, Tanaka S, Haga A, Nakamoto T, Suzuki Y, Mukasa A, Takayanagi S, Kitagawa Y, Hana T, Nejo T, Nomura M, Nakagawa K, Saito N. Radiomics Analysis for Glioma Malignancy Evaluation Using Diffusion Kurtosis and Tensor Imaging. Int J Radiat Oncol Biol Phys 2019;105:784-91. [Crossref] [PubMed]
27. Jenkinson M, Beckmann CF, Behrens TE, Woolrich MW, Smith SM. FSL. Neuroimage 2012;62:782-90. [Crossref] [PubMed]
28. Federau C, Meuli R. Brien K, Maeder P, Hagmann P. Perfusion measurement in brain gliomas with intravoxel incoherent motion MRI. AJNR Am J Neuroradiol 2014;35:256-62. [Crossref] [PubMed]
29. Press WH, T Teukolsky SA, Vetterling WT, Flannery BP. Numerical recipes: the art of scientific computing. 3rd edition. Cambridge: Cambridge University Press, 2007.
30. van Griethuysen JJM, Fedorov A, Parmar C, Hosny A, Aucoin N, Narayan V, Beets-Tan RGH, Fillion-Robin JC, Pieper S, Aerts HJWL. Computational Radiomics System to Decode the Radiographic Phenotype. Cancer Res 2017;77:e104-7. [Crossref] [PubMed]
31. Loizou CP, Pantziaris M, Seimenis I, Pattichis CS. Brain MR Image Normalization in Texture Analysis of Multiple Sclerosis. 2009 9th Internatianl Conference onInformation Technology and Applications in Biomedicine. Larnaca: IEEE, 2009:1-5.
32. Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, Blondel T, Prettenhofer P, Weiss R, Dubourg V, Vanderplas J, Passos A, Cournapeau D, Brucher M, Perrot M, Duchesnay E. Scikit-learn: Machine Learning in Python. Journal of Machine Learning Research 2011;12:2825-30.
33. Wolpert DH. Stacked generalization. Neural Networks 1992;5:241-59. [Crossref]
34. Nakamoto T, Takahashi W, Haga A, Takahashi S, Kiryu S, Nawa K, Ohta T, Ozaki S, Nozawa Y, Tanaka S, Mukasa A, Nakagawa K. Prediction of malignant glioma grades using contrast-enhanced T1-weighted and T2-weighted magnetic resonance images based on a radiomic analysis. Sci Rep 2019;9:19411. [Crossref] [PubMed]
35. Kallner A. Formulas. In: Laboratory Statistics. 2nd edition. Amsterdam: Elsevier, 2018:1-140.
36. DeLong ER, DeLong DM, Clarke-Pearson DL. Comparing the areas under two or more correlated receiver operating characteristic curves: a nonparametric approach. Biometrics 1988;44:837-45. [Crossref] [PubMed]
37. Zhou XH, Obuchowski NA, McClish DK. Statistical Methods in Diagnostic Medicine. 2nd edition. Hoboken, NJ, USA: John Wiley & Sons, Inc., 2011.
38. Sun X, Xu W. Fast Implementation of DeLong’s Algorithm for Comparing the Areas Under Correlated Receiver Operating Characteristic Curves. IEEE Signal Processing Letters 2014;21:1389-93. [Crossref]
39. Inano R, Oishi N, Kunieda T, Arakawa Y, Yamao Y, Shibata S, Kikuchi T, Fukuyama H, Miyamoto S. Voxel-based clustered imaging by multiparameter diffusion tensor images for glioma grading. Neuroimage Clin 2014;5:396-407. [Crossref] [PubMed]
40. Bishop CM. Pattern Recognition and Machine Learning. International Edition. Kolkata: Springer India, 2013.
41. Goodfellow I, Bengio Y, Courville A. Deep Learning. Cambridge, MA, USA: MIT Press, 2016.
42. Wen Q, Kelley DA, Banerjee S, Lupo JM, Chang SM, Xu D, Hess CP, Nelson SJ. Clinically feasible NODDI characterization of glioma using multiband EPI at 7 T. Neuroimage Clin 2015;9:291-9. [Crossref] [PubMed]
43. Lampinen B, Szczepankiewicz F, Mårtensson J, van Westen D, Sundgren PC, Nilsson M. Neurite density imaging versus imaging of microscopic anisotropy in diffusion MRI: A model comparison using spherical tensor encoding. Neuroimage 2017;147:517-31. [Crossref] [PubMed]
44. Wang Y, Wang Q, Haldar JP, Yeh FC, Xie M, Sun P, Tu TW, Trinkaus K, Klein RS, Cross AH, Song SK. Quantification of increased cellularity during inflammatory demyelination. Brain 2011;134:3590-601. [Crossref] [PubMed]